Français
Français
Understanding > Fundamental concepts > Phenomena II
RISE AND SET OF A CELESTIAL BODY
RISE AND SET OF THE SUN OR OF ANOTHER BODY
We have seen in the pages on
the seasons the notion of rotation of the Earth around its axis combined with its rotation around the Sun. The notion
of the "day" is then defined. We will see more precisely in the present page,
how to determinate rises and sets of the Sun, the Moon and the other celestial bodies.
Rise and set of a celestial body is an astronomical phenomenon calculated and predicted
from the ephemerides of the body.
In the case of the Sun, rises and sets define the day and the night. More simply,
the Sun sets when its decreasing height above the horizon becomes zero.
Similarly, the Sun rises when this height, increasing, becomes zero.
Two phenomena will make more complex this definition:
- What is the point of the Sun which will be taken into account for the calculation of its height? In fact, the Sun presents an apparent disk having a size of half a degree. The Sun sets when either the height of the center of the Sun or of the superior limb become zero.
- The atmospheric refraction makes the height of the celestial bodies higher than without atmosphere. So, thanks to the refraction, the Sun is still visible even it is actually under the horizon.
For the first point above, it is just a definition to choose. The ephemerides provide the position of the centre of the Sun and if we prefer to take into account the superior limb of the Sun, one will have to correct the position of the Sun of half its apparent disk, i.e. half a degree. In fact, the Sun is rarely visible on the horizon, except on the seashore, so that this difference is no very important.
For the second point we will have to take into account the refraction effect since it is the apparent Sun which is implied in its rise or set. The value of the refraction just at the horizon is difficult to determinate and we will take a value by convention, supposed to be the best for any location.
Some notions, that we will see latter, are related to the rise and set of the celestial bodies:
- the passage or transit across the meridian (superior) which is the instant where the object is at its higher height in the sky, in the direction of the South (for locations in the Northern hemisphere). The transit across the inferior meridian corresponds, for the Sun, to the instant in the night where the Sun is the lower under the horizon.
- the twilight which defines a period of time when it is neither night nor day. We define several twilight depending on the height of the Sun below the horizon: -6° for the civilian twilight, -12° for the nautical twilight and -18° for the astronomical twilight.
- theazimut at rise or at set defines the direction in which the Sun (or any object) will rise or set.
The calculation of the time of rise and set
Note : all the examples of calculation hereafter use the ephemerides published in the Annuaire du Bureau des longitudes for 1999.
To calculate the instant of rise and set of a celestial object for which we know the equatorial coordinates α and δ at the time of the phenomenon,
we calculate first the hour angle H at the time of the rise or of the set using the formula :
(1) cos H = (sin(h0) - sin(φ) sin(δ))/(cos(φ) cos (δ))
where φ is the latitude of the location and h0 a small angle which we will define latter.
An approach value of the sidereal time is then :
(2a) T = α - H
and of the set,
(2b) T = α + H
We calculate then, from T, the instant of the phenomenon
in Universal Time.
If the object is movong rapidly on the celestial sphere
(case of the Sun, some planets and mainly the Moon),
we calculate for the determinated instant the coordinates α and
δ more precise by interpolating the tables and we recalculate H then T,
using the formulae (1) and (2), so we get then the instant of the phenomenon
in UT. For the Moon it is necessary to make one more
iteration.
Concerning h0, it is given by :
h0 = P - R - 1/2 d - η1 + η2
P is the parallax which is negligeable for all bodies except
the Moon for which we will take it as 57'.
R is the refraction at horizon. The tables published in the
Annuaire du Bureau des longitudes use the theory of refraction by
Radau which provides R = 36' 36" but we could use the value
R = 34' adopted in the Nautical Ephemerides
published by the Bureau des Longitudes and also in the Nautical Almanac.
1/2 d is the apparent semi-diameter of the object. We put it in the formula
when calculating rise and set for the superior limb of the Sun and of the Moon
in place of the center of the disk. We take, either for the Sun or the Moon, 1/2 d =
16'.
If the observer is at an altitude A above the sea level
we introduce in h0 the angle η1 given by :
cos η1 = a / (a + A), where; a is the radius of the Earth.
We take a = 6 378 140 m. It is possible to use an approached formula :
η1 = 1' 56" square root of(A)
A given in meters.
If we look for rise and set of an object in a location
where the horizon is limited by mountains having an altitude of D situated
at a distance l from the observer, we will add to h0 the angle
η2 given by :
tan η2 = D/l .
It is not necessary to try to get the instants of rise and set of celestial objects
with an accuracy larger than one minute,
the true value of the refraction at horizon at the time of the phenomenon being known with a bad accuracy.
Examples
1. Set at Bordeaux of the star Sirius on 20 April 1999
The mean coordinates of the star for 1999 are :
α = 6h 45m 6s ; δ = - 16° 42' 53" .
Making the correction of precession in order to go to 20 April we find :
α = 6h 45m 7s ; δ = - 16° 42' 54" .
Here P = 0, 1/2 d = 0, η1 = 0, η2 = 0;
then: h0 = - R = - 34' .
The coordinates (longitude and latitude) of Bordeaux are :
λ = + 2m 7s ; φ = + 44° 50' 7" .
We deduce from formula (1) :
cos H = 0,28402 ; then H = 73,500° = 4h 54m 0s.
The sidereal time at set is :
T = α + H = 11h 39m 7s.
The sidereal time of Greenwich is then :
T1 = T + λ = 11h 41m 14s.
The sidereal time of Greenwich at 0h on 20 April 1999 is
T0 = 13h 50m 33s.
Then:
Tt = T1 - T0 = 21h 50m 41s.
Converting this interval of sidereal time into an interval
of mean time, we find that Sirius sets at Bordeaux on 20 April
1999 at :
t = 21h 47m 6s (UT).
2. Set of the superior limb of the Sun at Paris on 26 January 1999
We will take R = 34'.
Then :
h0 = - R - 1/2 d = - 50' .
The coordinates of Paris observatory are :
λ = - 9m 21s ; φ = 48° 50' 11".
The coordinates of the Sun at 0h on 26 January are
α = 20h 31m 44s ; δ = - 18° 52,6' .
Using formula (1) :
H = 68,4248° = 4h 33m 42s.
Then the sidereal time at set :
T = α + H = 25h 5m 26s.
at Greenwich T1 = T + λ = 24h 56m 5s.
On 26 January 1999 at 0h, the sidereal time at Greenwich is
T0 = 8h 19m 23s.
Then:
Tt = T1 - T0 = 16h 36m 42s.
In mean time it gives, as approximate time of set:
t = 16h 33m 59s (UT).
Let us calculate, interpolating the table of the ephemeris
provided by the
Annuaire du Bureau des longitudes, the coordinates
of the Sun at that time; we find :
α = 20h 34m 37s; δ = - 18° 42,2'.
Doing again the calculations using formula (1)
we find :
H = 68,6610° = 4h 34m 39s.
Then finally Tt = 16h 40m 32s.
That gives for the set t = 16h 37m 48s (UT).
We may verify that one more iteration will give the same result
which will be considered as definitive.
It appears that in the Annuaire du Bureau des longitudes the Sun set
is given at
16h 36m (UT). The difference ist due to the fact that in the table
we provide the set of the centre and that the refraction at horizon
was taken as 36' 36".
Approached instant of rise and set of a celestial object
The following formula provides the differences between the hour angles
at rise or at set of an object of declination δ, between a given location
having latitude φ and Paris (latitude φ0) :
Δ H = +/- 5,2min x {(φ - φ0)/(1 -0,03[φ -φ0])} x tan(1,8δ
+44')
où Δ φ = φ - φ0 is given in degrees
and Δ H in minutes of hour; the sign - corresponds to rise, the sign
+ to set.
The formula is valid, to the nearest 0,5 min, for δ included
between - 30° and + 30°. It allows the calculation, in Universal Time,
of rise and set of the Sun, for a location of latitude φ included between
+ 42° et + 54°. It is sufficient to add to the Universal Time of rise or set
at Paris a correction equal to L + Δ
H, L being the longitude of the location referred to the meridian of
Paris (counted from 0h to 12h, positively toward West).
For the Moon (in France, the declination of the Moon may
be chosen equal to the one corresponding to rise
or set at Paris) this correction must be multiplied
by the value of the lunar day for the considered date, converted in
mean day. The same calculous may be applied to planets
and stars; the correction L + Δ H must be multiplied
by the value of the day defined by the interval of two successive transits
of the celestial object at meridian, converted in mean day.
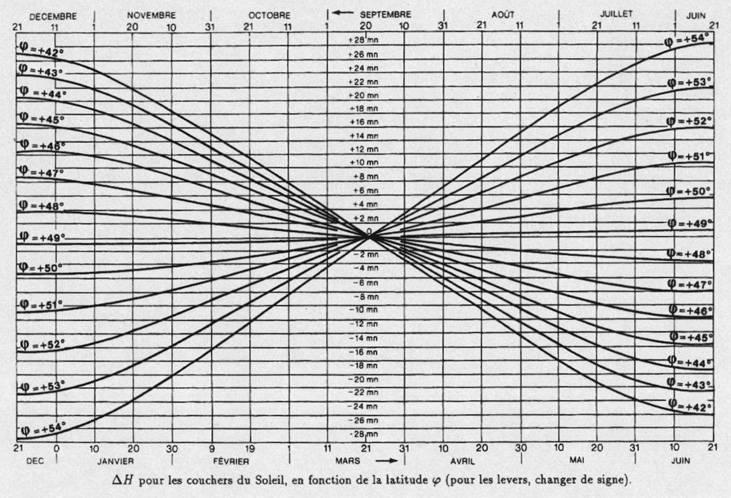
Concerning the Sun, we provide below, a graphical representation
giving the values of Δ H for latitudes included between
+ 42° and + 54°, depending on the date.
Azimut of a celestial object at its rise and at its set
The azimut a of a body of declination
δ at its set in a location of latitude φ (α and λ
are not useful in the present case) is given by :
cos h0 cos a = sin(h0) tan φ - {sin(δ)/ cos(φ))
The azimut at rise is the opposite of azimut at set.
EXAMPLE :
Determination of the azimut of the Sun at Paris on 26 January 1999
at its set.
We have :
cos h0 cos a = sin(h0) tan φ - {sin(δ)/ cos(φ))
cos a = 0,4690 and a is near 62,0°
(a between 180° and 360° for a rise, between 0° and 180°
for a set).
Variation of the instant of Sun rise and Sun set in France
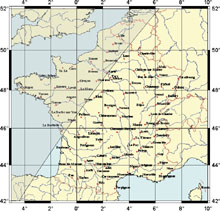
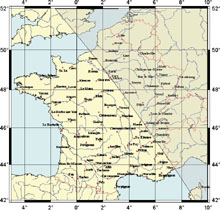
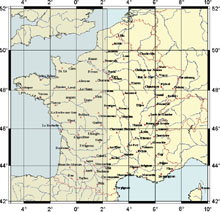
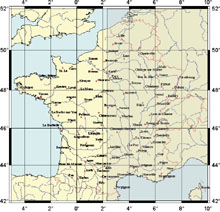
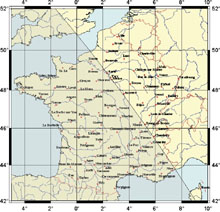
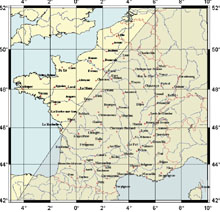
Everybody knows that the Sun does not rise at the same time at Paris, at Brest or at Nice. How this difference evolutes? Is it constant all along the year ? In fact, two parameters are involved, longitude and latitude of the considered location. For the longitude, it is easy to understand that Eastern territories see the Sun before the others. For the latitude, it is known that in summer, more we go North, longer is daylight, i.e. Sun rises earlier and sets latter. It is the contrary in winter. Both parameters are combined so that at the solstice, the Sun rises at the same time at Paris and at Nice but the Sun sets earlier at Nice than at Paris. Maps below (click on them for enlarging) show where the Sun rises and sets at the same time than in Paris for the dates of the solstices and for the Spring equinox. The darker zones correspond to where the Sun is set.
LIGHT ON EARTH FROM THE SUN
Duration of the day
We name "day" (different from the day, unit of time equal to 24 hours) the interval of time
between the Sunrise and the Sunset for a given location.
The longest day takes place at the summer solstice in the Northern hemisphere
and at the winter solstice in the Southern hemisphere. The shirtest day takes place
at the other solstice.
The next table provides the maximal and minimal duration of the day for
several latitudes.
| Latitude |
Day maximal | Day minimal |
|---|---|---|
| 0° | 12h 05m | 12h 05m |
| 10° | 12h 40m | 11h 30m |
| 20° | 13h 18m | 10h 53m |
| 30° | 14h 02m | 10h 10m |
| 40° | 14h 58m | 9h 16m |
| 45° | 15h 33m | 8h 42m |
| 50° | 16h 18m | 8h 0m |
| 55° | 17h 17m | 7h 5m |
| 60° | 18h 45m | 5h 45m |
| 65° | 21h 43m | 3h 22m |
| 66° | 24h 0m | 2h 30m |
| 67° 7' | 0h 0m |
On the equator, the duration of the day is larger than 12 h because of the refraction which shows us the Sun when it is below the horizon.
For the high latitudes, there is no Sunset (or no Sunrise) when the algebric sum
(or the difference) of its declination
and of the latitude of the location is at least equal to 90° in
absolute value.
So, we have the polar day (or polar night) the durations of which are given
in the table below.
| Northern latitude |
Polar day | Polar night |
|---|---|---|
| 70° | 70 days | 55 days |
| 75° | 107 days | 93 days |
| 80° | 137 days | 123 days |
| 85° | 163 days | 150 days |
| 90° | 189 days | 176 days |
| Southern latitude |
Polar day | Polar night |
|---|---|---|
| 70° | 65 days | 59 days |
| 75° | 101 days | 99 days |
| 80° | 130 days | 130 days |
| 85° | 156 days | 158 days |
| 90° | 182 days | 183 days |
Twilight
In astronomie, we name twilight the increasing light, before Sunrise, decreasing after Sunset, coming from the light of the Sun being below the horizon, in the upper atmosphere. In the common language, the morning twilight is named dawn or aurora.
The evening twilight, for example, starts at Sunset and ends when the center of the Sun is below the horizon of an angle h. Three twilights may be defined: the civilian twilight (h = 6°), the nautical twilight (h = 12°), and the astronomical twilight (h = 18°).
In order to know the instant of the beginning or of the end of twilight
we may use the formula (1) provided in the section dedicated to rises and sets above :
cos H = (sin(h0) - sin(φ) sin(δ))/ (cos(φ) cos (δ))
In this formula h0 will be equal to - 6° for the
civilian twilight, - 12° for the nautical twilight, and - 18° for
the astronomical twilight; δ is the declination of the Sun at its set or at its rise.
We then calculate, as we did for the rise and the set
Tt = α +/- H + λ - T0,
where α is the right ascension of the Sun at rise or at set,
λ the longitude of the location, and T0 the sidereal time of Greenwich
at 0h of the considered day; we use the sign - for a beginning of twilight
and the sign + for an end of twilight.
EXAMPLE :
End of the civilian twilight at Paris on 26 January 1999
.We have seen previously that the Sunset at
Paris at this date took place at 16h 37m 48s UT and that the
coordinates of the Sun at this instant were :
α = 20h 34m 37s, ; δ = - 18° 42.2'.
Taking, h0 = - 6° (civilian twilight).
We have H = 77.3172° = 5h 9m 16s.
We deduce that Tt = 17h 15m 9s and, by converting this interval
in sidereal time into mean time, that the end of the
civilian twilight on 26 January 1999 takes place at 17h 12m 19s UT.
The civilian twilight has the following duration :
17h 12m 19s - 16h 37m 48s = 34m 31s.
In order to avoid the previous calculus, it is possible, after the
calculation of rise or set, to calculate the beginning or the end of the twilight
by substracting (for a rise) or adding (for a set)
the duration of the twilight as given in the tables and graphical representations below.
Civilian, nautical and astronomical twilight :
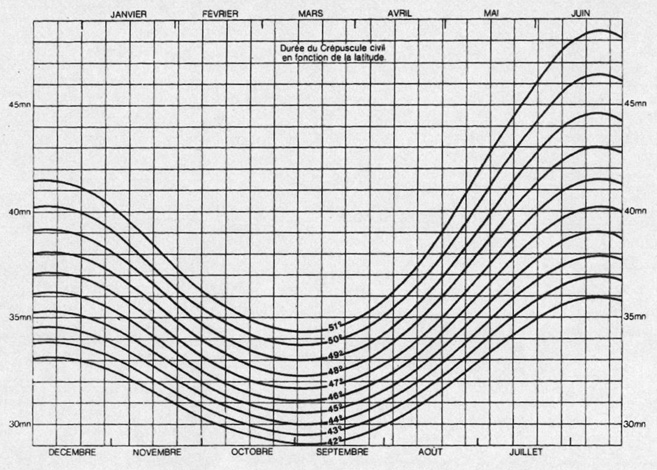
Civilian twilight. --- It starts on the evening after Sunset and ends when the Sun is 6° below the horizon. At that time, if the weather is clear, stars and planets of "first magnitude" appear. In the morning, the phenomenon is opposite.
The Sun does not go more than 6° below the horizon when
the algebric sum of its declination and of the latitude of the location
is at least equal to 84° in absolute value.
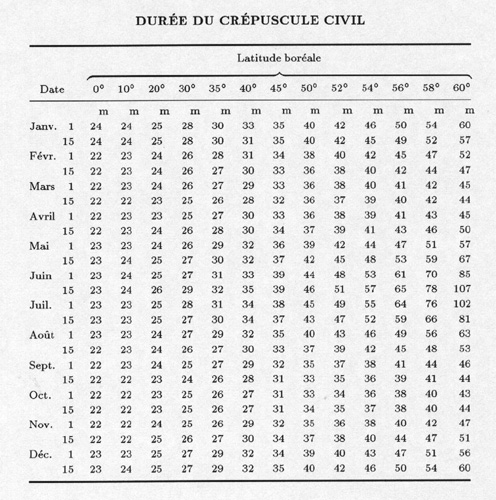
Information concerning the duration of the civilian twilight
as a function of the latitude are provided by the table andb graphical
representation below. The first table provides for the northern latitudes
from 0° to 60°, the duration, in
minutes, of the civilian twilight. The same table may be used for southern
latitudes, by adding or substracting
6 months to the date.
The following graphical representation gives directly this
duration for northern latitudes
from 42° to 51°. The vertical lines indicate time intervals of 8 days.
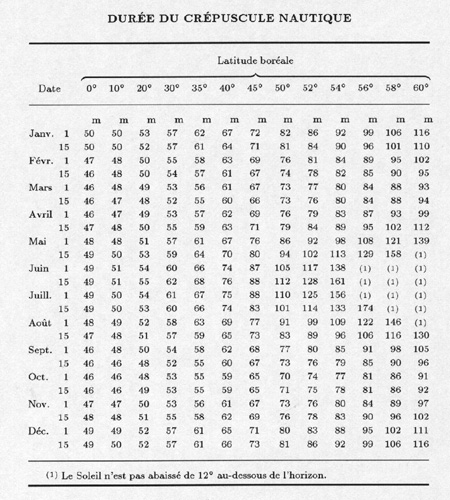
Nautical twilight. --- It starts at the evening after Sunset and ends when the center
of the Sun reaches 12° below the horizon. At this time, if the weather is clear,
stars of "second magnitude" starts to appear and the line horizon is still visible.
In the morning, the phenomenon is opposite.
The Sun does not go more than 12° below the horizon when
the algebric sum of its declination and of the latitude of the location
is at least equal to 78° in absolute value.
The table below provides, for the northern latitudes
from 0° to 60°, the duration in minutes,
of the nautical twilight. The same table may be used
for southern latitudes by adding or substracting
6 months to the date.
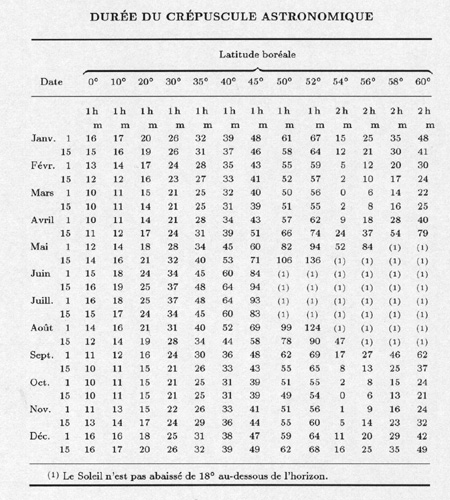
Astronomical twilight. --- It starts on the evening after the Sunset
and ends when the ceneter of the Sun go mote than
18° below the horizon. At this time, if the weather is clear,
stars until the sixth magnitude become visible and night arrives.
In the morning, the phenomenon is opposite.
The Sun does not go more than 18° below the horizon when
the algebric sum of its declination and of the latitude of the location
is at least equal to 72° in absolute value.
Information concerning the duration of the astronomical twilight
as a function of the latitude are provided by the table below which provides for the northern latitudes
from 0° to 60°, the duration, in
minutes, of the astronomical twilight.
The same table may be used for southern
latitudes, by adding or substracting
6 months to the date.
Credit : IMCCE/BDL
Click here to access to the calculation of rises and sets of Sun and planets.