


 Français
Français
Understanding > Fundamental concepts > Tides
THE TIDES (this section is written in French)
LES MAREES
- Aperçu qualitatif
- Les théories antiques
- Les historiens et les philosophes
- Les docteurs de l'Église
- Les physiciens du XVIIe siècle
- D'autres théories plus au moins fantaisistes
- La marée statique de Newton (1642 - 1727)
- La théorie dynamique de Laplace
- Un peu d'histoire
- Aujourd'hui
- Données numériques
- Bibliographie
Aperçu qualitatif
Le phénomène de marée met en évidence deux faits importants :
-si la Terre attire la Lune, la Lune attire aussi la Terre : la gravitation est une inter-action entre 2 corps
-l'attraction gravitationnelle entre 2 points dépend de leur distance ; comme les différents endroits d'un océan sont à différentes distances de la Lune, ils subissent une attraction différente.
D'après le Petit Robert la marée est un « mouvement journalier d'oscillation de la mer, dont le niveau monte et descend alternativement en un même lieu, provoqué par l'attraction de la Lune et du Soleil ». Cette définition rend parfaitement compte du phénomène, mais mérite d'être précisée.
Tout d'abord, le phénomène, journalier au sens où il a lieu tous les jours, présente plus volontiers, p.ex. sur les côtes atlantiques, une période de l'ordre de 12 h 25 min, soit la moitié de la période apparente de rotation de la Lune, et non 12 heures, ce qui serait la signature d'un phénomène dû au soleil.
Donc, pour une 1ère compréhension du phénomène de marée, on s'intéressera surtout à l'action de la Lune sur la Terre. Et l'on va se limiter tout d'abord à une description statique, en admettant que l'oscillation résulte ensuite de la simple rotation apparente de la Lune autour de la Terre. Et puis, en ayant remarqué qu'une flaque d'eau ne subit guère de marée, même lorsqu'elle est grande comme la Mer Méditerranée, on s'intéressera à la marée à l'échelle planétaire, en allant jusqu'à supposer la présence d'un océan couvrant uniformément toute la Terre (c'est en fait vrai à 78%).
En l'absence de la Lune, cet océan global et exagéré ressemblerait à ceci :

La Lune étant présente, elle exerce sur différents points de la Terre une force dirigée vers le barycentre lunaire, et d'autant plus faible que le point est éloigné de la Terre. On s'intéresse à l'interaction au centre de la Terre, et en différents points de l'océan (échelles non respectées) ; la Lune, non représentée, serait à l'intersection des supports des vecteurs forces.
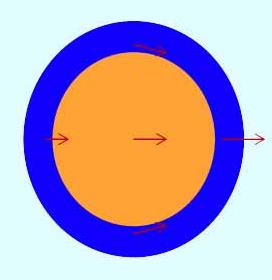
Le schéma précédent montre une Terre globalement attirée par la Lune, ce qui est juste du point de vue de la Lune, mais trompeur de notre point de vue d'observateur terrien. Pour reconsidérer ce point de vue de la Terre, et en supposant la Terre en fait très lourde par rapport à la Lune (le rapport des masses vaut 81 en faveur de la Terre), l'attraction lunaire sur le barycentre de la Terre est nulle.
Ce changement de point de vue s'appelle, en physique, un changement de référentiel. Il conduit à la vision schématique, dérivée de la figure précédente, où à chaque flèche a été retranchée celle correspondant à l'action au centre de la Terre.
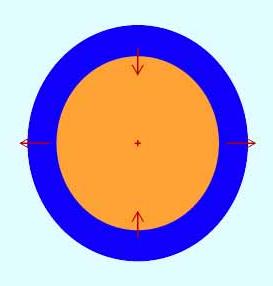
Ces flèches représentent l'action de la Lune en divers points du globe terrestre. Sous l'action de ces forces, l'océan, fluide, va prendre une position d'équilibre le déformant légèrement, avec 2 bourrelets respectivement dirigés vers et à l'opposé de la Lune.
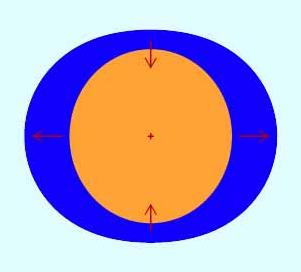
Et l'on comprend qu'il suffit alors de faire tourner la Terre sur elle-même et la Lune autour de la Terre pour animer le mouvement des marées. Comme il y a 2 bourrelets, il y a aura 2 marées hautes et 2 marées basses par période de 24 h 50 min.
Evidemment, lorsque l'on reprend toutes les hypothèses émises, la compréhension profonde et l'interprétation du phénomène se compliquent. Ceci fait l'objet de la suite de l'exposé.
Les théories antiques
Les historiens et les philosophes
Dans l'antiquité de nombreuses explications ont été
proposées pour expliquer le phénomène des marées.
On peut retenir que le phénomène était en général
bien décrit, mais que les explications ont été très
liées à la physique aristotélicienne. Dans le "Timée"
(~VIe siècle av. J.C.), on pense que les fleuves poussent
la mer et créent les marées. Platon
(~429 - ~347 av. J. C.), pense que les eaux entrent et sortent
d'un gouffre. Héraclide (388 - 315 av.
J. C.), suppose que la Lune et le Soleil sont à l'origine
des marées. Aristote (384 - 322 av. J.
C.), pense que c'est l'écrasement des eaux du fond de
la mer par les eaux de surface. Pline l'Ancien
(v 23 - 79) dans son Histoire Naturelle, décrit
correctement le phénomène et pense que la marée est
liée à la Lune et au Soleil "Sur la nature des eaux, enfin,
beaucoup a déjà été dit; mais cette avance
et le retrait des flots sont les plus extraordinaires; cependant si ce
phénomène offre beaucoup de variété, sa cause
réside dans le Soleil et dans la Lune ", il observe les deux
marées par jour "Entre deux levers de la Lune, la mer monte deux
fois et redescend deux fois dans chaque intervalle de 24 heures " puis
il remarque que "Jamais les marées ne se reproduisent au même
moment que le jour précèdent, comme si elles haletaient par
la faute de l'astre avide qui attire à lui les mers pour s'abreuver.".
Il décrit également fort bien le décalage de temps
entre les pleines mers et le passage au méridien de la Lune (l'établissement)
"les phénomènes célestes faisant toujours sentir
leurs effets à la Terre avec du retard sur la vue, comme l'éclair,
le tonnerre ou la foudre", il décrit la corrélation entre
les marées de vives-eaux et les syzygies et entre les marées
de mortes-eaux et les quadratures "Au moment de la conjonction, elles
égalent les marées de pleine Lune".
Il remarque également la plus forte amplitude
des marées d'équinoxe, "Tout cela est augmenté
par les influences annuelles du Soleil". Dans cette remarquable description
du phénomène il ne manque que l'observation de l'âge
de la marée, phénomène difficilement observable sans
la connaissance des instants précis des syzygies.
Les docteurs de l'Église
Saint Augustin (354 -430), puis Saint Thomas d'Aquin (1225 - 1274) attribuent également l'origine des marées à la Lune.
Mais chez tous, si la description est exacte, l'explication physique est fausse.
À partir d'Aristote, l'explication est la suivante :
l'eau de la Lune attire l'eau de la Terre suivant le principe de sympathie entre les corps.
Les physiciens du XVIIe siècle
Kepler (1571 - 1630) explique le phénomène, mais utilise encore le principe de sympathie.
Galilée (1564 - 1642) se sert des marées pour prouver la rotation de la Terre autour du Soleil et autour d'elle-même. Il fait un raisonnement circulaire,les marées sont dues à la rotation terrestre sur elle-même, et comme les marées existent, la Terre tourne sur elle-même. Il suppose que les points de la sphère terrestre sont animés de vitesses variables. Il combine les vitesses de rotation et de translation terrestres. Ces différences de vitesse engendrent des accélérations à l'origine des marées. Ce raisonnement est faux car la vitesse de translation est négligeable devant la vitesse de rotation.
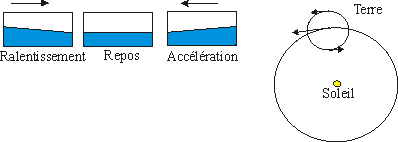
Pour expliquer les vives-eaux et les mortes-eaux, il fait intervenir la Lune en utilisant une analogie avec le mouvement pendulaire :
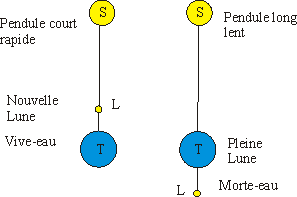
Dans le cas de la pleine Lune " le balancier" du pendule est plus long qu'à la nouvelle Lune, il y a donc pour une même courte période de temps une vitesse variable du couple Terre-Lune donc des marées différentes, mais de nouveau le raisonnement bien que logique est contraire à l'observation, car les marées de vives-eaux ont lieux à la fois à la pleine Lune et à la nouvelle Lune, alors que l'explication pendulaire devrait engendrer des marées de mortes-eaux à la pleine Lune.
D'autres théories plus au moins fantaisistes
Le Père Georges Fournier (1595 - 1652) aumônier de la Flotte Royale, démontre les erreurs de Galilée, mais propose une théorie délirante " plus proche des diagnostics des médecins de Molière que d'une recherche d'hydrographie" (A. Gillet, 1998) : les marées sont dues aux humeurs de la Terre soignées par la lumière solaire!
César d'Arçons ( ? - 1681) explique la marée à l'aide d'un mouvement de va-et-vient de la Terre le long de l'axe du monde.
Scalberge Minière dans son traité sur les marées utilise la dilatation des mers par le Soleil. La Lune jouant un rôle de miroir.
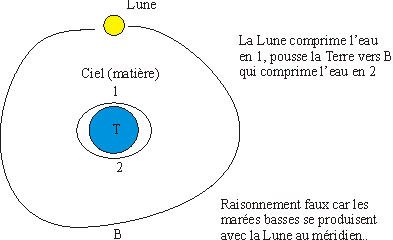
Descartes (1596 - 1650)a une explication cohérente mais toute aussi fausse que celle de Galilée. Il relie les astres par de la matière et les fait se déplacer par des tourbillons. La Lune comprime la matière du ciel qui écrase l'eau.
La marée statique de Newton (1642 - 1727)
Les observations de l'époque
Sur les côtes atlantiques deux marées par jour,
décalées de 12h 24m environ. Soit 48 minutes de décalage
par jour dues au mouvement de la Lune. La marée haute est liée
au passage de la Lune au méridien, mais décalée dans
le temps (établissement du port).
Les marées de vives-eaux correspondent aux syzygies
et les marées de mortes-eaux correspondent aux quadratures.
Pour un lieu donné, les marées de vives-eaux
n'ont pas lieu exactement aux syzygies mais sont légèrement
décalées (âge de la marée).
Les marées d'équinoxes sont plus fortes
(grandes marées).
La théorie
Newton explique le phénomène des marées
à l'aide de la gravitation universelle. La figure d'équilibre
d'une sphère liquide sous l'action d'un corps céleste (Lune
ou Soleil) est un ellipsoïde de révolution dont le grand-axe
est orienté vers le corps.
Il prend pour hypothèse dans un premier temps
que le corps perturbateur est dans le plan équatorial de la Terre,
puis dans un second cas que le corps n'est plus dans l'équateur
terrestre.
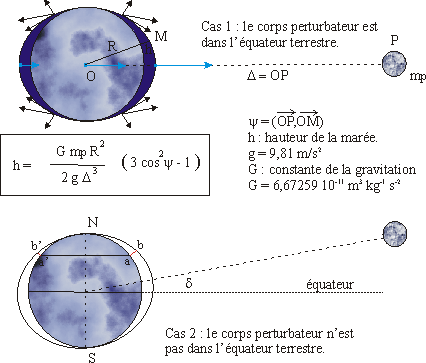
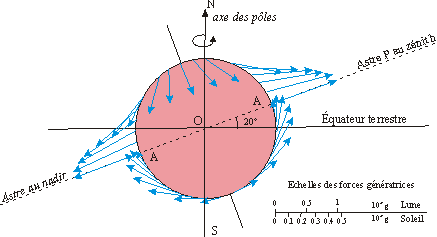
On trouve bien un ellipsoïde comme figure d'équilibre
dans le cas de la perturbation lunaire et un autre ellipsoïde dans
le cas de la perturbation solaire la figure d'équilibre est la combinaison
de ces deux ellipsoïdes.
Il trouve que la hauteur de la marée liée
à l'action de la Lune est h Lune = 0,35m et la hauteur
de la marée liée au Soleil est h Soleil = 0,16m,
le rapport de ces deux quantités étant de h Lune/h
Soleil= 2,2.
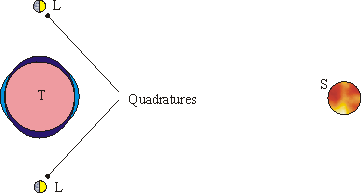
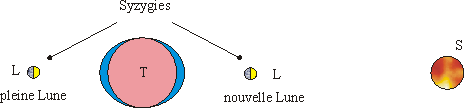
Cette théorie explique parfaitement la corrélation entre les marées de vives-eaux et les syzygies et les marées de mortes-eaux et les quadratures.
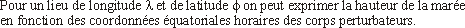
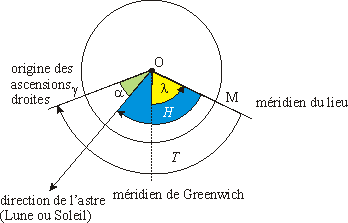
où

avec
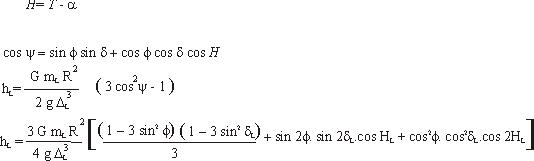
On a une formule identique pour le Soleil
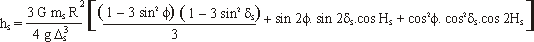
Si l'on applique les valeurs numériques des paramètres
physiques et orbitaux de la Lune et du Soleil dans ces deux formules, on trouve que l'amplitude de hL
est d'environ 34cm et que l'amplitude de hS est d'environ 16cm.
Le mouvement apparent du Soleil est de 24h (Soleil moyen)
et le mouvement apparent de la Lune est de 24h 48m (Lune moyenne).
On constate que les hauteurs sont proportionnelles à
la masse des corps perturbateurs et inversement proportionnelles au cube
des distances à la Terre. Les effets s'ajoutent lorsque les angles
horaires de la Lune et du Soleil sont égaux ou diffèrent
de 180° (syzygies). Les effets sont minimum lorsqu'ils sont déphasés
de 90° donc aux quadratures. La hauteur est maximale (vives-eaux) lorsque
l'astre est au méridien.
Chacune de ces deux formules peut se décomposer en trois termes :
-
Un terme semi-diurne en cos 2H de coefficient
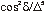
-
Un terme diurne en cos H de coefficient

- Un terme à longue période ne dépendant pas de H mais dépendant de sinδ au carré donc de période 14 jours pour la Lune et 6 mois pour le Soleil.
δ varie de -23° à +23° pour le Soleil et de -28° à + 28° pour la Lune, ce terme est maximal lorsque le Soleil et la Lune sont proches de l'équateur. La variation de hauteur est de 15% pour le Soleil et 22% pour la Lune.
La hauteur varie comme sin 2δ, donc de 0 à 0.83 pour la Lune et 0 à 0.72 pour le Soleil, ce terme est nul aux équinoxes mais aussi lorsque le lieu est sur l'équateur. La hauteur croit avec la latitude.
On remarque que le terme semi-diurne ne s'annule jamais et que le terme diurne s'annule aux équinoxes et à l'équateur.
L'échec de la théorie statique.
1- Les hauteurs observées (13 mètres au Mont Saint Michel) sont très différentes des hauteurs prévues (maximum 50cm).
2- L'inégalité diurne n'est pas nulle dans les zones équatoriales, au contraire elle est très forte. Par contre aux fortes latitudes, où elle devrait être forte, elle est quasi inexistante ( par exemple dans la marée atlantique)
3- Pour un lieu donné on observe un retard entre les syzygies et les marées de vives-eaux et également un retard entre les quadratures et les marées de mortes-eaux (âge de la marée). On observe également un retard entre le passage au méridien de l'astre et l'heure de la marée de vives-eaux (établissement du port).
En conclusion les hypothèses de la marée statique sont trop simplificatrices, la marée est un phénomène dynamique. De plus dans la théorie statique on ne tient pas compte des continents.
La théorie dynamique de Laplace (1749 - 1827)
La rotation terrestre demande au bourrelet d'eau, pour suivre
l'astre perturbateur, de se déplacer par rapport aux fonds marins.
Il y a donc deux mouvements, un mouvement vertical qui constitue la marée
et un mouvement horizontal qui constitue le courant de marée. Les
bassins océaniques étant fermés, il va se créer
des phénomènes de réflexions des ondes stationnaires
et des phénomènes de résonances lorsque la période
d'oscillation des bassins océaniques sera en phase avec la période
de la marée astronomique (diurne ou semi-diurne).
À chaque port correspond un régime particulier de marée.
Les formules précédentes restent valables, mais les coefficients et les phases doivent être déterminés expérimentalement à partir des observations des hauteurs de marées pour un lieu donné.
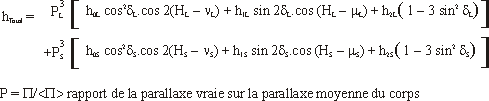
Les dix paramètres sont déterminés par une analyse en fréquence des variations des hauteurs observées.
Ainsi pour le port de Brest on trouve :
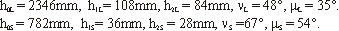
Les rapports hiL/hiS sont égaux à 3, ce qui est en accord avec la théorie statique (2,2)
Les termes semi-diurnes sont prépondérants
devant les termes diurnes (22 fois plus grand).
Les valeurs vL
et vS donnent l'établissement
du port (48° + 67°)/2 = 57,5° soit 3h 50m environ et leur différence
permet de calculer l'âge de la marée (67°- 48°) =
19°, la phase varie de 19° en 37,4 h (29,5j/360° x 19°)
donc l'âge de la marée est de 37,4h.
La réalité est encore plus complexe car
on doit tenir compte de tous les harmoniques, on doit ajouter d'autres
ondes de périodes plus petites, les ondes quart-diurne, semi-tiers-diurne...
ainsi que des termes à longue période (termes annuels, semi-annuels,
mensuels...)
On utilise 143 ondes élémentaires. Pour
Brest, si on se limite aux termes générant une amplitude
supérieure au millimètre on ne conserve que 105 termes. L'utilisation
de toutes ces fréquences permet d'expliquer des phénomènes
locaux particuliers ainsi l'onde sixième diurne est en certain lieu
à l'origine de l'inégalité dans la durée entre
le montant et le perdant qui provoque une tenue de plein, par exemple au Havre.
L'explication de la résonance semi-diurne en Atlantique nord, s'explique par les dimensions du bassin océanique. Lorsque la longueur d'onde est très supérieure à la profondeur du bassin, la vitesse de propagation de l'onde est donnée par : v = (g.z) ½ où g est l'accélération de la pesanteur (9.81m/s2) et z la profondeur du bassin. La période d'oscillation N correspondant à un aller retour de l'intumescence est égale à v = 2L/N donc N = 2L/(g.z) ½ où L est la longueur du bassin (formule de Mérian). Dans le cas de l'Atlantique nord on a : L ~ 4000km, z ~ 3000m, donc N ~ 12,8h donc en phase et en résonance avec l'onde semi-diurne lunaire de 12,4h.
La marée est donc décomposée en séries d'harmoniques obtenues par analyse en fréquence des variations des niveaux de la mer en un lieu donné.
Ces harmoniques sont généralement répartis en quatre groupes
- Les harmoniques semi-diurnes de périodes voisines de 12h.
- Les harmoniques diurnes de périodes voisines de 24h.
- Les harmoniques de longues périodes : bimensuelle, mensuelle, semestrielle, annuelle...
- Les harmoniques supérieures et composées de périodes quart-diurne, tiers-diurne...
Les différents types de marées
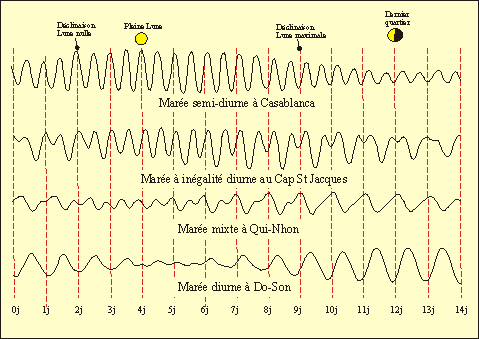
On distingue
Les marées semi-diurnes : les harmoniques diurnes sont négligeables devant les harmoniques
semi-diurnes. Il y a donc deux marées par jour, d'importance égale.Exemple : l'océan Atlantique.
Les marées semi-diurnes
à inégalité diurne : les harmoniques diurnes
ne sont plus négligeables devant les harmoniques semi-diurnes. On
a encore deux pleines mers et deux basses mers par jour, mais les hauteurs
de ces marées peuvent être très différentes
(Cap St Jacques, océan Indien et certaines parties du Pacifique).
Les marées mixtes : les harmoniques diurnes prédominent, mais les harmoniques semi-diurnes
apparaissent en fonction de la valeur de la déclinaison de la Lune.
On a ainsi deux marées par jour lorsque la Lune est proche de l'équateur
(décl. = 0) et une seule marée par jour lorsque la déclinaison
de la Lune est proche de son maximum (Indonésie, Viêt-Nam,
Antilles, côtes de Sibérie et Alaska).
Les marées diurnes : les harmoniques semi-diurnes sont négligeables devant les harmoniques
diurnes, on n'a alors qu'une marée par jour (océan Pacifique
et côtes de Sibérie orientale, golfe du Tonkin).
Trois cartes issues du serveur du SHOM, montrent les différentes
zones où l'on trouve ces quatre types de marée : cliquer
ci-après pour visualiser ces cartes :
- l'Atlantique et la Méditerranée,
- l'océan Indien et l'Océanie,
- le Pacifique
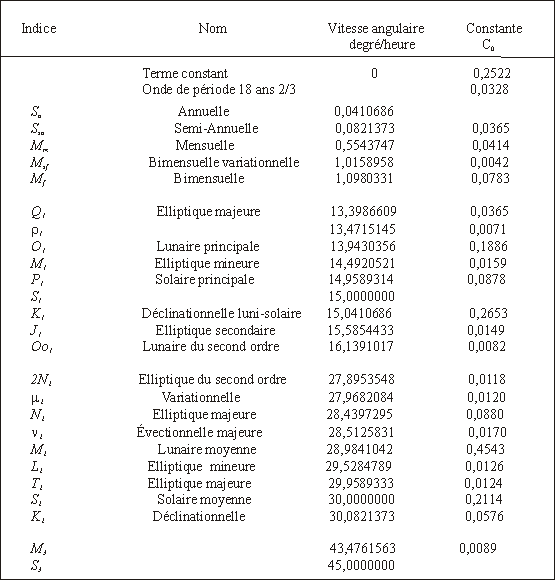
La solution réelle est bien évidemment plus complexe, et comme on l'a vu précédemment on doit tenir compte de nombreux termes dans les développements harmoniques. Le tableau suivant donne la listes des harmoniques principaux; le coefficient C0 est le poids moyen de lâharmonique dans le développement du potentiel générateur. (source : Encyclopédie du BdL).
Aspect des cartes de marées :
Sur les cartes de marées, on trace les lignes isophases
(points où la marée a lieu au même instant), ces lignes
portent le nom de lignes cotidales, on porte également sur ces cartes
les lignes où les hauteurs sont égales, ce sont les lignes
isomarnages. Les lignes cotidales se coupent et rayonnent autour des points
amphidromiques. Ces points peuvent être réels (en mer) où
virtuels (à Terre, le marnage est nul donc la phase est indéterminée).
Les lignes cotidales tournent dans le sens inverse des aiguilles d'une
montre dans l'hémisphère nord (liées aux forces de Coriolis).
Pour visualiser la carte représentant l'évolution
de la marée dans l'Atlantique nord au voisinage des côtes
françaises, cliquer ici.
Le marnage
Le terme marnage désigne la différence de hauteur
de la marée entre une pleine mer et une basse mer successives. Le
marnage est fort durant les périodes de vives-eaux et faible durant
les périodes de mortes-eaux. Les marnages peuvent être très
différents d'une région géographique à l'autre.
Le marnage maximal observé dans le monde est dans
la baie de Fundy, au Canada entre la Nouvelle-Écosse et le Nouveau-Brunswick.
Le marnage peut y atteindre jusqu'à 16m.
En France, dans la baie du Mont-Saint-Michel, le marnage peut atteindre jusqu'à 12 - 13m par forts coefficients.
Trois cartes, issues du serveur du SHOM, montrent les
marnages moyens observés à travers le monde : cliquer
ci-après pour les visualiser :
- l'Atlantique et la Méditerranée,
- l'océan Indien et l'Océanie,
- le Pacifique.
Un peu d'histoire
La méthode des harmoniques utilisée de nos
jours, a été imaginée dès le milieu du XIXe
siècle par lâingénieur hydrographe Rémi Chazallon
(1802 - 1872). Cet ingénieur est également à l'origine
d'un appareil d'enregistrement de la marée : le marégraphe.
En France, le premier annuaire des marées a été publié
en 1839. Les hauteurs des marées étaient publiées
en pieds et en pouces. Les anglais publièrent un annuaire dès
l'année suivante en 1840 (William Whewell).
La première machine à calcul verra le jour
en 1873, elle est l'oeuvre de Sir William Thomson (lord Kelvin 1824 - 1907)
sur une suggestion de Beauchamp de la Tour.

Credit : Droits réservés
Cette machine permettait de faire la somme des 10 composantes harmoniques principales.
D'autres machines plus performantes furent construites
par la suite. En 1910, une machine permettant de sommer les 37 harmoniques
principaux et permettant également de tracer la hauteur de la marée
fut mise en service au United State Coast and Geodetic Survey. En France
on utilisera une machine de ce type jusqu'en 1960.
Aujourd'hui
L'apparition des ordinateurs et de l'altimétrie par
satellites a profondément modifié l'étude théorique
de la marée.
Les ordinateurs ont remplacé les machines de prédictions
de marées. De plus leur puissance de calcul permet de prendre en
compte un très grand nombre de paramètres.
Les satellites permettent de mesurer la hauteur des océans
sur tout le globe terrestre avec une précision de l'ordre de 2cm.
De nos jours, l'aspect général de la marée
peut être pris en compte, les modèles théoriques s'appliquent
au mouvement global des océans. On ne se limite plus à l'aspect
et à la prédiction de la marée locale.
Pour cela, on doit tenir compte de la totalité
des phénomènes qui modifient cette hauteur. Les modèles
sont donc très complexes.
Quelques données numériques
Rayon moyen de la Terre : 6371 km.
Masse de la Terre : 5,9736 x 1024 kg.
Masse du système Terre-Lune : 6,0471 x 1024
kg
Masse de la Lune : 0,0735 x 1024 kg.
Masse du Soleil : 1,9889 x 1030 kg.
Constante de la gravitation : G = : 6,67259 10-11
m3kg-1 s-2.
Superficie du globe terrestre : 510 x 106
km2.
Accélération de la pesanteur moyenne : g = 9,806 m/s2.
Vitesse angulaire de rotation de la Terre : v = 0,72921
x 10-4 rad/s =15,0410°/h.
Durée du jour sidéral : 23h 56min 4s (de
temps solaire moyen).
Superficie des océans et des mers : 361 x 106
km2 (71% de la surface terrestre).
Volume des mers : 1370 x 106 km3.
Profondeur moyenne des océans : environ 3800m.
Profondeur maximale dans les océans (fosse des
Mariannes) : 11520m, soit 1/553 du rayon terrestre moyen.
Densité moyenne des eaux océaniques (ramenée
à la pression atmosphérique) : 1,0276
Température moyenne des eaux marines : t = 3,52°C.
Salinité moyenne des eaux marines : S = 34,72
p. 1000.
Masse des sels marins : 4,8 x 1019 kg.
Poids moyen de sel marin par unité de surface
océanique : 133 t/m2 ou 13,3 kg/cm2.
Masse des eaux océaniques : 1,40 x 1021
kg soit 0,234 millième de la masse terrestre.
Poids moyen d'eau par unité de surface marine : 388 kg/cm2.
Poids moyen d'eau par unité de surface du globe : 275 kg/cm2.
Les océans contiennent 97% de l'eau de la surface
du globe.
La vapeur d'eau atmosphérique est d'origine marine
pour 85%, d'origine continentale pour 15%.
Bibliographie
Encyclopédie scientifique de l'univers - Bureau des longitudes -volume : La Terre, les eaux, l'atmosphère, 1984, Gauthiers Villars, Montreuil.
Les Guides du SHOM, La marée, 1997, SHOM, Brest.
Une histoire des marées, André Gillet, 1998, Belin Paris.
Sur Internet :
Le site du SHOM : http : //www.shom.frPour les sites CNES et NASA consulter les liens du site du SHOM.
Credit : P. Rocher, B. Mosser/observatoire de Paris



