THE LAWS OF KEPLER

Kepler's laws are derived only from the observation of the motion of planets: they represent a kinematic description of this motion without making any assumptions about the nature of the forces involved. Kepler (1571-1630) was a disciple of Tycho Brahe (1546-1601) whom he succeeded as astronomer of the German Emperor Rudolf II. Tycho Brahe is mainly an observer of precise positions of the planets but if he made very good observations, however, he was not convinced by the heliocentric theories of Copernicus (1473-1543). He still thinks that the Earth is the center of the solar system. Kepler will use the observations of Tycho Brahe to state his laws. Kepler was convinced that Copernicus was right, which will be definitely demonstrated by Galileo (1564-1642) in 1610 through the use of a telescope and the observation of the satellites of Jupiter.

Kepler states his first two laws in 1609:

- each planet described in the forward direction, an ellipse whom one of the focus is occupied by the Sun.
Until then, only the circle was considered as a possible trajectory of celestial bodies. These are the precise observations of Tycho Brahe which allowed to abandon this assumption. The ellipticity of the orbits of the planets is very small. The difference between the circle and the orbit of the Earth is very tiny: if we wish to represent it on a sheet of paper, the difference between the circle and the ellipse lies in the thickness of the pencil! Fortunately the Sun is not the center of the ellipse, but at the focus that makes a difference.
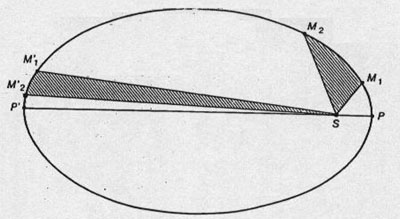
- areas described by the planet-Sun radius vector is proportional to the time used to describe them.
The meaning of this law is clear: the planets do not rotate with a uniform velocity. They are faster when they are closer to the Sun and slower when they are far. This is particularly observable with comets whose orbits are, unlike those of the planets, highly eccentric (very elongated).

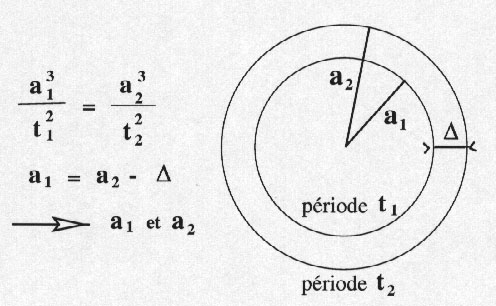
The law of areas : the areas described by the mobile in equal times are equal. So when the body moves away from the Sun, its velocity decreases.

Kepler stated his third law in 1619:

- the cube of the semi-major axis "a" of an orbit of a planet, divided by the square of the orbital period T (sidereal) is a constant for all planets in the solar system.
That is to say :
a³/T² = constant or n²a³ = constant (n being the mean motion = 2π/T)
This law relates the planets together. In fact, this law comes from the predominant mass of the Sun in the Solar System. We will see that the law of gravitation generates a force proportional to the masses involved. In the case of the solar system, the masses of the planets are negligible compared to that of the Sun and the above constant is the product of the solar mass and the gravitational constant.

Kepler could not demonstrate its laws: he lacked the fundamental principles of mechanics and the Newton's law, i.e. the foundations of dynamics, which, when applied to the celestial bodies, form the celestial mechanics. Kepler introduced the concept of elliptical path that will completely change the model of the solar system.

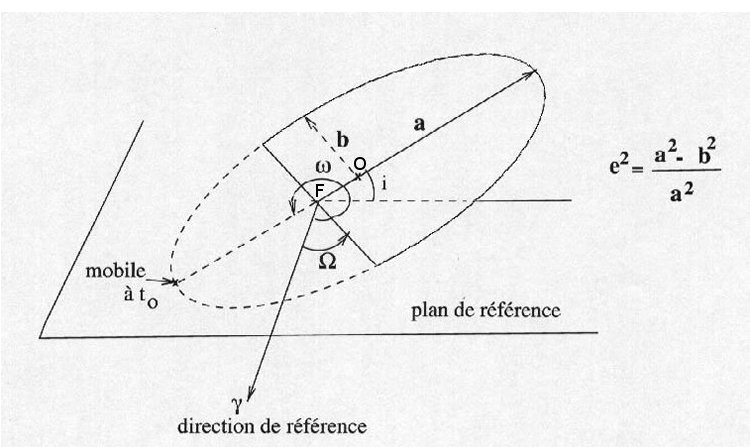
Parameters of the ellipse

To define an elliptical path, it requires six parameters:

-the semi-major axis a
-the eccentricity e such as e²=(a²-b²)/a² où b is the semi-minor axis. We have : OF= a e .
-the inclination i on the plane of reference (equateur or ecliptic)
-the longitude of the ascending node on the reference plane
-the longitude of the periapsis (point of the path the closest to the central body) counted from the ascending node or from a fixed direction (equinox)
-the date of the passage of the body at the periapsis t₀ or the mean anomaly M=n(t-t₀) where n=2π/T with T period of revolution defined by the 3^rd law of Kepler (stating that n² a³ is a known constant).

How to define an ellipse in space (O is the center and F the focus).

Celestial mechanics and the distances in the solar system

Kepler's laws give us an extremely powerful model to determine distances in the solar system. We have seen that the simple observation of solar system bodies allows us to obtain only the Earth-Moon distance. The Earth-Sun distance is too large to be measured accurately using parallax. Kepler's laws will help us. As we have seen, the mean motion n (=2π/T) and the semi-major axis are linked. So if you know one distance in the solar system, you know all the others as shown in the following figure.

Measuring distances in the solar system by measuring the distance to the near passage of any body

Historically, the first distance measured in the solar system was not the Earth-Sun distance. For this determination, we measured the distance from Earth to Mars. The first observation of this distance took place in 1672 when passing close to Mars, then it was the distance from Earth to Venus during the transits of Venus across the Sun where the parallax effect is particularly noticeable for two distant observers.

The transits of Venus across the Sun are on horizontal lines and are seen at different heights depending on the place of observation on Earth: we can deduce the distance Earth-Venus from such observations.

During the 1930s, astronomers measured the distance between Earth and Eros (an asteroid passing close to Earth). Today, shooting radar on Mars, Venus, Mercury give the distances with high accuracy. We then deduce all distances of the planets by observing their period of revolution around the Sun. Astronomers defined as a unit of distance the semi-major axis of a body whose period is 365.2568983263 days. It's almost Earth, but not really as the unit of distance in the solar system should not depend on improvements in the theory of motion of the Earth.

Credit : J.E. Arlot/IMCCE