LES LOIS DE KEPLER

Les lois de Kepler ne découlent que de l'observation du mouvement des astres : elles ne représentent qu'une description cinématique de ce mouvement sans faire d'hypothèses sur la nature des forces en jeu. Kepler (1571-1630) est le disciple de Tycho Brahe (1546-1601) auquel il succède comme astronome de l'empereur d'Allemagne Rodolphe II. Tycho Brahe est principalement un observateur de positions précises mais s'il effectue de très bonnes observations, en revanche, il n'est pas convaincu par les théories héliocentriques de Copernic (1473-1543). Il pense toujours que la Terre est au centre du système solaire. Kepler va utiliser les observations de Tycho Brahe pour énoncer ses lois. Kepler est convaincu que Copernic a raison, ce qui sera définitivement démontré par Galilée (1564-1642) en 1610 grâce à l'utilisation d'une lunette astronomique et à l'observation des satellites de Jupiter.

Kepler énonce ses deux premières lois en 1609 :

-chaque planète décrit, dans le sens direct, une ellipse dont le Soleil occupe l'un des foyers.
Jusqu'alors, on n'avait considéré que le cercle comme trajectoire possible des corps céleste. Ce sont les observations précises de Tycho Brahe qui ont permis de revenir sur ce postulat. L'ellipticité des orbites des planètes est très faible. La différence entre le cercle et l'orbite de la Terre est infime : si on veut la représenter sur une feuille de papier, la différence entre le cercle et l'ellipse tient dans l'épaisseur du trait de crayon ! Heureusement le Soleil n'est pas au centre de l'ellipse, mais au foyer qui est décentré.
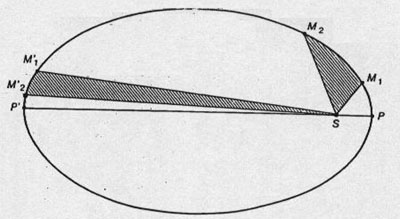
-les aires décrites par le rayon vecteur planète-Soleil sont proportionnelles aux temps employés pour les décrire.
La signification de cette loi est claire : les planètes ne tournent pas avec une vitesse uniforme : elles vont plus vite quand elles sont près du Soleil et plus lentement quand elles en sont loin. Cela est particulièrement observable pour les comètes dont les orbites sont, contrairement à celles des planètes, très excentriques (très allongées).

La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales. Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitessediminue.

Kepler énonce sa troisième loi en 1619 :

-le cube du demi grand axe a d'une orbite d'une planète, divisé par le carré de la période de révolution T (sidérale) est une constante pour toutes les planètes du système solaire.
C'est-à-dire :
a³/T² = constante ou bien n²a³ = constante (n étant le moyen mouvement = 2π/T)
Cette loi relie les planètes entre elles. En fait, cette loi provient de la masse prépondérante du Soleil dans le système solaire. On verra que la loi de la gravitation engendre une force proportionnelle aux masses en jeu. Dans le cas du système solaire, les masses des planètes sont négligeables devant celle du Soleil et la constante ci-dessus est le produit de la masse solaire et de la constante de la gravitation.

Kepler ne pouvait pas démontrer ses lois : il lui manquait les principes fondamentaux de la mécanique ainsi que la loi de Newton, c'est-à-dire les fondements de la dynamique, qui, appliqués aux astres, forment la mécanique céleste. Kepler introduit la notion de trajectoire elliptique qui va complètement modifier la modélisation du système solaire.

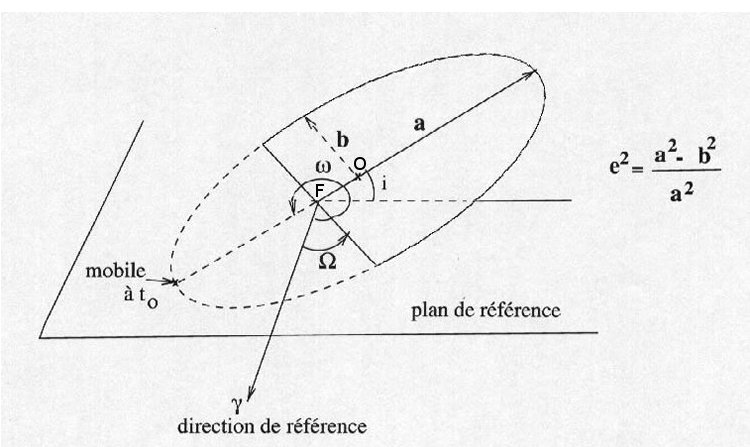
Les paramètres de l'ellipse

Pour définir une trajectoire elliptique, on a besoin de six paramètres :

-le demi-grand axe a
-l'excentricité e telle que e²=(a²-b²)/a² où b est le demi-petit axe. On a : OF= a e .
-l'inclinaison i sur un plan de référence (équateur ou écliptique)
-la longitude du noeud ascendant sur le plan de référence
-la longitude du périastre (point de la trajectoire le plus proche du corps central) comptée à partir du noeud ascendant ou d'une direction fixe (équinoxe)
-l'instant de passage du corps au périastre t₀ ou l'anomalie moyenne M=n(t-t₀) où n=2π/T avec T période de révolution définie par la 3^ème loi de Kepler (qui dit que n² a³ est une constante connue).

Comment repérer une ellipse dans l'espace (O est le centre et F le foyer).

La mécanique céleste et les distances dans le système solaire

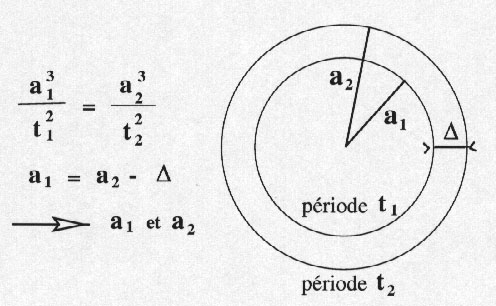
Les lois de Kepler nous fournissent un modèle extrêmement puissant pour déterminer les distances dans le système solaire. Nous avons vu que l'observation simple des corps du système solaire ne nous permet d'obtenir que la distance Terre-Lune. La distance Terre-Soleil est trop grande pour la mesurer avec précision à l'aide de la parallaxe. Les lois de Kepler vont nous aider. Comme nous venons de le voir, le moyen mouvement n (=2π/T) et le demi-grand axe sont liés : donc si on connaît une distance dans le système solaire, on connaît toutes les autres comme le montre le shéma suivant.

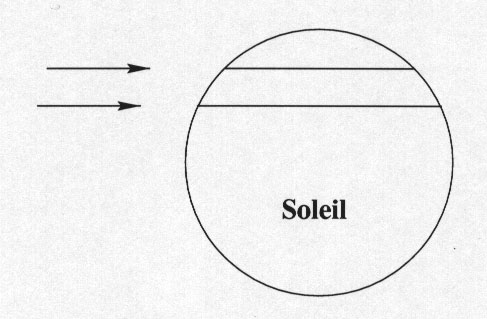
Mesure des distances dans le système solaire par la mesure de distance au passage proche d'un autre corps

Historiquement, la première distance mesurée dans le système solaire ne fut pas la distance Terre-Soleil. Pour cette détermination, on mesura la distance Terre-Mars. La première observation de cette distance eut lieu en 1672 lors du passage proche de Mars, puis ce fut la distance Terre-Vénus lors des passages de Vénus devant le Soleil où l'effet de parallaxe est particulièrement visible pour deux observateurs éloignés.

Les passages de Vénus devant le Soleil se font sur des cordes horizontales et sont vus différemment selon le lieu d'observation sur Terre : on en déduit la distance Terre-Vénus

Vers 1930, on a mesuré la distance Terre-Eros (astéroïde passant au plus près de la Terre). Aujourd'hui, on réalise des tirs radar sur Mars, Vénus, Mercure qui donnent la distance avec précision. On en déduit alors toutes les distances des planètes en observant leur demi-grand axe en unités angulaires et leur période. On se définit comme unité de distance le demi-grand axe d'un corps dont la période est 365,2568983263 jours. C'est presque la Terre, mais pas vraiment car l'unité de distance dans le système solaire ne doit pas dépendre des améliorations de la théorie du mouvement de la Terre.

Crédit : J.E. ArlotIMCCE