








 English
English
Comprendre > Concepts fondamentaux > Phénomènes VII
Passages des planètes Mercure et Vénus devant le Soleil
Sommaire
- I. Introduction
- II. Explication du phénomène: l'aspect géométrique
- III. Critères pour qu'un passage soit observable, périodicité
- IV. Le calcul des passages
- V. La construction des canons des passages de Mercure et de Vénus devant le Soleil
- VI. L'observation des passages de Mercure et Vénus devant le Soleil
I. Introduction
Les passages de Mercure et Vénus devant le Soleil, sont des phénomènes
rares qui ont été observés par les astronomes depuis
plusieurs siècles (voir à ce sujet la page
sur l'historique de l'observation des passages).
Aujourd'hui, ils sont surtout une curiosité attendue impatiemment
par les astronomes amateurs.
Les prochains passages auront lieu :
Parmi les corps du système solaire de taille importante, seules la Lune et les planètes Mercure et Vénus peuvent passer devant le Soleil pour un observateur terrestre. Si, dans le cas de la Lune le phénomène (éclipse de Soleil) est courant, il n'en est pas de même pour Mercure et Vénus : le phénomène de passage devant le Soleil est rare. Il est, bien sûr, moins spectaculaire qu'une éclipse de Soleil : le diamètre apparent maximum de Mercure est en effet de l'ordre de 1/200ème de celui du Soleil et celui de Vénus est de l'ordre de 1/30ème. Dans le cas de Vénus, le passage est aisément observable à l'oeil nu, moyennant quelques précautions pour la protection des yeux. La méthode d'observation par projection de l'image solaire sur un écran blanc est la meilleure.
Ainsi d'un point de vue purement calculatoire, le calcul d'un passage de Mercure ou de Vénus devant le Soleil est identique au calcul d'une éclipse de Soleil par la Lune. Bien évidemment compte tenu des diamètres apparents de ces deux planètes "l'éclipse" est toujours annulaire ou partielle.
II. Explication du phénomène: l'aspect géométrique
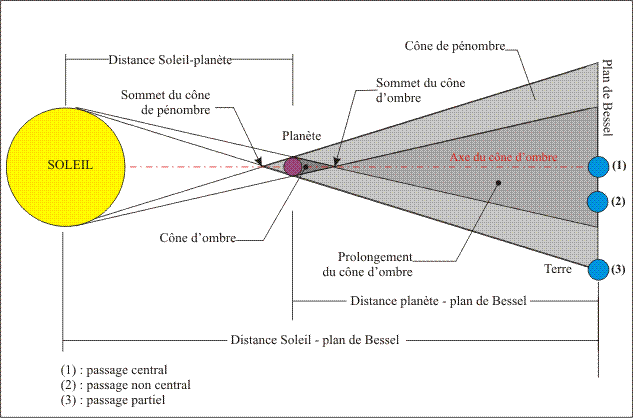
Les planètes Mercure et Vénus, éclairées par le Soleil, donnent naissance, dans la direction opposée au Soleil à deux cônes, un cône d'ombre et un cône de pénombre. La droite joignant le centre du Soleil et le centre de la planète constitue l'axe de ces cônes. Le sommet du cône de pénombre est situé sur cet axe entre le Soleil et la planète, et le sommet du cône d'ombre est également situé sur cet axe mais de l'autre côté par rapport à la planète. Pour un observateur placé dans le cône d'ombre, avant son sommet il y a éclipse totale du Soleil par la planète, pour un observateur situé dans le prolongement du cône d'ombre, donc après le sommet du cône d'ombre, il y a éclipse annulaire du Soleil par la planète, donc passage de la planète devant le Soleil. Lorsqu'un observateur se trouve dans le cône de pénombre, il assiste à une éclipse partielle, donc un passage partiel de la planète devant le Soleil. En raison des distances entre la Terre et ces deux planètes, la Terre passe uniquement dans le prolongement du cône d'ombre et dans le cône de pénombre. Cela se traduit pour un observateur terrestre par l'observation d'un passage de la planète devant le disque solaire (éclipse annulaire) compris entre deux phases partielles. On peut également avoir uniquement un passage de la Terre dans la pénombre, dans ce cas on n'observe qu'une phase partielle d'éclipse, donc le passage d'une partie du disque de la planète sur le disque solaire.
Si les orbites des planètes Mercure et Vénus étaient dans le plan de l'écliptique (plan de l'orbite de la Terre), il y aurait un passage des planètes devant le Soleil chaque fois que les planètes sont en conjonction en longitude avec la Terre, donc avec des périodicités égales aux révolutions synodiques des deux planètes. La révolution synodique est l'intervalle de temps qui s'écoule entre deux passages successifs d'une planète dans une position déterminée par rapport au Soleil et à la Terre (conjonction ou opposition). L'inclinaison de l'orbite de Mercure (~7°) et de Vénus (~3,39°) limite la possibilité des passages aux voisinages de la ligne des noeuds des orbites. La ligne des noeuds est la droite formée par l'intersection du plan de la planète et le plan de l'orbite terrestre.
Le plan de Bessel est le plan passant par le centre de la Terre et normal à l'axe des cônes. Les intersections des cônes d'ombre et de pénombre avec le plan de Bessel déterminent des cercles d'ombre et de pénombre. La comparaison des rayons de ces cercles avec la distance entre l'axe des cônes et le centre de la Terre permet de savoir si le centre de la Terre pénètre dans les cônes d'ombre et de pénombre, donc de savoir si le passage est observable ou non.
Si les planètes avaient des trajectoires circulaires autour du Soleil, la géométrie du problème serait figée et les tailles des cônes d'ombre et de pénombre, ainsi que la position de leurs sommets, seraient constantes dans le temps. En réalité les planètes parcourent des trajectoires elliptiques perturbées et les distances Soleil-planètes ne sont pas constantes. Les plus grandes valeurs des angles au sommet des cônes d'ombre et de pénombre des planètes correspondent aux minima des distances Soleil-planètes (planètes au périhélie) et les plus petites valeurs correspondent aux maxima des distances Soleil-planètes (planètes à l'aphélie). En réalité comme les passages ne sont observables qu'au voisinage des noeuds des orbites, il convient de calculer les dimensions des cônes d'ombre et de pénombre au voisinage des noeuds des orbites des planètes. En raison des perturbations les lignes des noeuds des planètes, ainsi que les lignes des apsides (ligne joignant le périhélie et l'aphélie), ne sont pas fixes, mais sont animées de faibles mouvements de précession. La période de révolution correspondant à deux passages de la planète par le même noeud de l'orbite s'appelle la révolution draconitique et la période de révolution correspondant à deux passages de la planète à son périhélie s'appelle la révolution anomalistique de la planète. Pour le calcul des passages on doit utiliser des éléments moyens donnés dans le repère moyen de la date, le mouvement des lignes des noeuds et des lignes des apsides contiennent donc la précession, ce qui explique leurs mouvements apparemment directs alors qu'ils sont faiblement rétrogrades dans un repère fixe.
Le tableau suivant donne les valeurs moyennes des éléments elliptiques (Simon et al., 1994) des orbites de Mercure et Vénus dans le repère moyen de la date ainsi que les périodes moyennes des révolutions tropiques et synodiques de ces planètes calculées à l'aide de ces éléments. La révolution tropique d'une planète est l'intervalle de temps qui s'écoule entre deux passages de la planète dans la direction de l'équinoxe de printemps.
| Mercure |
Vénus | Terre | |
|---|---|---|---|
| demi-grand axe | 0.387098 ua | 0.723330 ua | 1.000001 ua |
| excentricité | 0.205632 | 0.006772 | 0.016709 |
| inclinaison | 7.004986 | 3.394662° | 0° |
| longitude du noeud | 48.330893° | 76.679920° | --- |
| longitude du périhélie | 77.456119° | 131.563703° | 102.937348° |
| moyen mouvement | 4.092377°/jour | 1.602169°/jour | 0.985647°/jour |
| révolution tropique | 87.968434 jours | 224.695435 jours | 365.2421904 jours |
| révolution synodique | 115.877477 jours | 583.921361 jours | --- |
Le tableau suivant donne pour les planètes les mouvements moyens des lignes des noeuds et des apsides ainsi que les périodes moyennes des révolutions draconitiques et anomalistiques dans le repère moyen de la date.
| Mercure |
Vénus | Terre | |
|---|---|---|---|
| mouvement moyen du noeud | 42.700014"/an | 32.437576"/an | 0"/an |
| mouvement moyen du périgée | 56.03043"/an | 50.47747"/an | 61.900553"/an |
| révolution draconitique moyenne | 87.969132 jours | 224.698895 jours | 365.2421904 jours |
| révolution anomalistique moyenne | 87.969350 jours | 224.700819 jours | 365.259636 jours |
Les passages de Mercure ont lieu aux voisinages des passages de la Terre par le noeud ascendant et par le noeud descendant de l'orbite de Mercure. Entre 1400 et 2600, la Terre passe par le noeud ascendant de l'orbite de Mercure dans la première moitié du mois de novembre et par le noeud descendant dans la première moitié du mois de mai.
De même les passages de Vénus ont lieu aux voisinages des passages de la Terre par les noeuds de l'orbite de Vénus. Entre 1200 et 2800, la Terre passe par le noeud ascendant de l'orbite de Vénus dans la première moitié du mois de juin et par le noeud descendant dans la première moitié du mois de décembre.
III. Critères pour qu'un passage soit possible, périodicité
Si les passages peuvent avoir lieu à certaines dates précises
dans l'année, ils ne se produiront pas à chaque fois. Il
se passe le même phénomène que dans
le cas des éclipses de Soleil: les inclinaisons relatives des
plans des orbites ne permettent pas un phénomène à
chaque interposition de la planète entre la Terre et le Soleil.
Dans le cas de Mercure, ils sont possibles en mai lorsque Mercure passe
par le noeud descendant de son orbite
et en novembre lorsque Mercure passe par le noeud ascendant de son orbite.
Cependant, lors des passages de mai , Mercure est proche de son aphélie
et se déplace donc plus lentement; au moment du passage au noeud,
la Terre, vue du Soleil doit être à une distance angulaire
inférieure à 108' pour que l'on puisse observer le passage.
Par contre pour les passages de novembre, la vitesse de Mercure sur son
orbite est plus forte et la Terre, toujours vue du Soleil , doit être
à une distance angulaire inférieure à 238' pour que
l'on puisse observer le passage. Donc le nombre de passages observables
en novembre seront statistiquement environ deux fois plus nombreux que
les passages observables en mai. Si l'on étudie les dates des passages
de Mercure devant le Soleil, on peut mettre en évidence des périodes
de récurrences de ces passages. Il existe une période de
46 ans et une période de 217 ans. On peut, comme pour les éclipses
du Soleil, construire des séries longues de passages espacés
de 46 ou 217 ans. Ainsi le passage du 15 novembre 1999 est le dernier d'une
série, le passage précèdent appartement à cette
série est celui du 14 novembre 1953.
Dans le cas de Vénus, on peut faire un calcul analogue, mais
son orbite plus grande et son mouvement plus lent diminue considérablement
le nombre de passages. Ces passages sont observables soit au voisinage
du noeud ascendant de l'orbite de Vénus vers le 9 décembre,
dans ce cas la Terre, vue du Soleil, doit avoir au moment du passage de
Vénus à son noeud, une distance angulaire inférieure
à 37' pour que le passage soit observable; soit au voisinage du
noeud descendant de l'orbite de Vénus vers le 7 juin, en ce cas,
la Terre, vue du Soleil doit avoir au moment du passage de Vénus
à son noeud, une distance angulaire inférieure à 41'
pour que le passage soit observable. Les périodes de révolutions
de la Terre et de Vénus sont prédominantes dans la fréquence
des passages observables. On met en évidence le cycle suivant 8
ans, 121.5 ans, 8 ans, 105.5 ans pour les passages observables de Vénus.

IV. Le calcul des passages
1. Les méthodes employées
Par le passé, lorsque les calculs étaient faits à la main, on se contentait de calculer les phases géocentriques des passages, c'est-à-dire les instants des entrées et des sorties du centre de la Terre des cônes de pénombre et d'ombre. Et l'on traçait sur un planisphère les limites de visibilité du phénomène, c'est-à-dire les courbes des lieux ayant la planète à l'horizon au moment de l'entrée et de la sortie du cône de pénombre. On calculait également le minimum de distance angulaire géocentrique entre le centre du Soleil et le centre de la planète, ce minimum caractérisant en quelque sorte la grandeur du passage. Pour l'édition des instants des différentes phases géocentriques, et pour des raisons de symétrie, on se limitait souvent à donner l'instant du minimum du passage et les demi-durées des phases d'ombre et de pénombre. Lorsqu'on se limite aux calculs des phases géocentriques, on ne trouve pas les passages partiels ne couvrant qu'un demi-hémisphère terrestre et ne passant pas par le centre de la Terre.
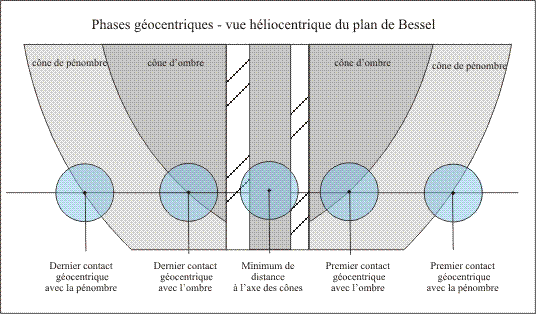
De nos jours, grâce à l'informatisation des calculs, il est possible de faire des calculs plus rigoureux et de déterminer les instants et positions des différents contacts entre les cônes d'ombre et de pénombre et la surface de l'ellipsoïde terrestre. Ces instants sont les phases générales du passage. Chaque phase, comme pour les éclipses de Soleil, correspond à un instant particulier et à un lieu bien défini sur la Terre. Ces phases générales tiennent compte des parallaxes solaire et planétaire.
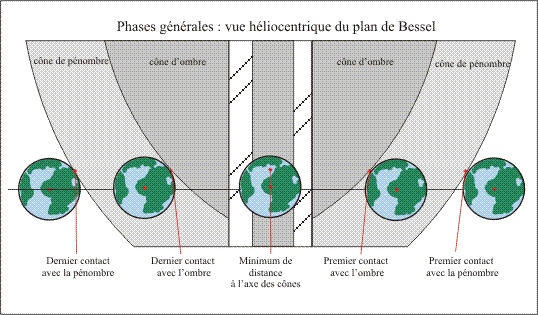
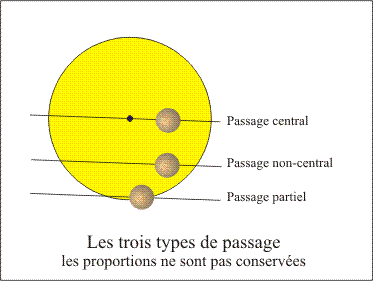
Les phases générales sont légèrement plus longues que les phases géocentriques, les différences de durée correspondent au temps mis par l'ombre ou la pénombre pour passer du point de contact au centre de la Terre. Ces écarts ne sont pas constants, mais varient avec les vitesses relatives de la planète et de la Terre et avec la position des points de contact sur les bords de l'ombre et de la pénombre. Les différences de tailles entre les rayons des cônes d'ombre et de pénombre montrent qu'il peut y avoir des passages où la Terre passe uniquement dans le cône de pénombre, dans ce cas on observe de la Terre un passage partiel du disque de la planète sur le disque solaire. Lorsque la Terre rencontre l'axe des cônes, il existe des lieux sur Terre où la planète lors de son passage devant le Soleil passe exactement par le centre du disque solaire, ces passages seront notés passages centraux. Tous les autres passages, et ce sont les plus fréquents, sont des passages non-centraux.
En conclusion, il y a trois types de passages, les passages centraux, les passages non-centraux et les passages partiels.
2. Les cartes
Les limites de visibilité des débuts et fins des différentes phases correspondent aux cercles terminateurs avant pour pôles les directions des lieux ayant la planète au zénith. Pour chaque phase considérée, ces limites sont les lieux ayant la planète à l'horizon. Les instants des différentes phases géocentriques et topocentriques étant relativement proches, les tracés de toutes ces courbes sur une même carte sont peu lisibles. C'est pourquoi, on se contente de tracer le début et la fin de la phase de pénombre. On peut tracer soit les phases géocentriques, soit les phases générales, la différence entre ces deux courbes est faible (surtout pour les passages de Mercure). En général, les revues anglo-saxonnes donnent les phases géocentriques; pour notre part, dans les documents fournis par l'Institut de mécanique céleste, nous traçons les phases générales ainsi que la phase maximale (minimum de distance). Dans le cas de Mercure on ne donne que les limites d'entrée et de sortie de la pénombre et la phase maximale, pour Vénus on donne les limites des entrées et des sorties de la pénombre et de l'ombre ainsi que la phase maximale.
Sur ces cartes on trace également les limites australes ou boréales du bord de l'ombre ou de la pénombre lorsqu'elles existent.
3. Les circonstances locales
On appelle circonstances locales d'un passage pour un lieu situé à la surface de la Terre les paramètres utiles à l'observation locale du passage. Ces paramètres sont :
- Les coordonnées géographiques du lieu (sa longitude et sa latitude).
- Le nom du lieu.
- La durée totale du passage en ce lieu.
- L'instant du maximum du passage en Temps universel (instant où dist. est minimale).
- dist. : la distance minimale entre le centre du Soleil et de la planète.
- h : la hauteur apparente du centre du Soleil (on ne tient pas compte de la réfraction athmosphérique).
- a : l'azimut apparent du centre du Soleil (attention, il s'agit de l'azimut des astronomes et non celui des marins).
- Les paramètres du premier contact extérieur.
- Les paramètres du premier contact intérieur.
- Les paramètres du dernier contact intérieur.
- Les paramètres du dernier contact extérieur.
Pour chaque contact, on donne successivement : l'instant du contact en Temps universel, les valeurs de l'angle au pôle P et de l'angle au zénith Z du point de contact. Si le contact n'existe pas ces données sont remplacées par des points.
L'angle au pôle P d'un contact est l'angle ayant pour sommet le centre du Soleil et pour côtés la direction du pôle nord céleste et la direction du contact. Il est compté positivement vers l'est à partir de la direction du pôle céleste. L'orbite de Mercure et de Vénus n'étant pas dans le plan de l'équateur céleste, les contacts extérieurs et intérieurs ne se situent pas obligatoirement de part et d'autre de la direction du pôle céleste nord.
L'angle au zénith Z d'un contact est l'angle ayant pour sommet le centre du Soleil et pour côtés la direction du zénith et la direction du contact. Il est compté positivement vers l'est à partir de la direction du zénith.
V. La construction des canons des passages de Mercure et de Vénus devant le Soleil
1. Paramètres et théories utilisés
Nous avons construit deux canons des passages de Mercure et de Vénus devant le Soleil, un par planète, portant sur la période -2999 (3000 av. J.-C.) à 3000 après J.-C.
Pour le calcul de ces canons nous avons utilisé les paramètres physiques suivants :
- la parallaxe horizontale du Soleil à une unité astronomique = 8.794148".
- le demi-diamètre solaire = 15´ 59.63".
- le rapport du rayon de Mercure sur le rayon équatorial terrestre : k = 0.3825096.
- le rapport du rayon de Vénus sur le rayon équatorial terrestre : k = 0.9488346.
- le rayon équatorial terrestre = 6378140m.
- le carré de l'ellipticité de l'ellipsoïde terrestre = 0.00669438.
Pour le calcul des éphémérides des planètes Mercure, Vénus et la Terre nous avons utilisé les théories suivantes :
- Les théories planétaires SLP98 sous forme de séries de polynômes de Tchebychev produites par G. Francou à partir des théories planétaires VSOP87 (P. Bretagnon et G. Francou, 1988).
- La théorie de la précession de Lieske (1976).
- La théorie de la nutation de Wahr (1981).
- La formule du calcul du temps sidéral d'Aoki (1992).
- Pour les époques anciennes, la différence entre le temps universel (UT) et le temps terrestre (TT) est calculée à l'aide des formules fournies par J. Chapront, M. Chapront et G. Francou (1997). Pour les époques futures cette différence est extrapolée à partir des dernières valeurs connues.
2. Statistiques sur les canons
Le tableau suivant donne les statistiques sur les canons des passages.
| Canon |
Passages de Mercure | Passages de Vénus |
|---|---|---|
| Nombre de passages centraux | 2 | 3 |
| Nombre de passages non-centraux | 796 | 76 |
| Nombre de passages partiels | 11 | 3 |
| Nombre de passages au noeud descendant | 255 | 45 |
| Nombre de passages au noeud ascendant | 554 | 37 |
| Nombre total de passage | 809 | 82 |
On remarque que les prévisions déduites des caractéristiques sur les tailles des critères de visibilité se vérifient. Ainsi pour Mercure on a 2.173 fois plus de passages au noeud ascendant qu'au noeud descendant, le rapport L0 ascendant sur L0 descendant donnait 2.125. De même pour Vénus on a 1.21 fois plus de passages au noeud descendant qu'au noeud ascendant le rapport L0 descendant sur L0 ascendant est égale à 1.13.
Pour le calcul de ce canon nous avons utilisé les paramètres physiques suivants :
- la parallaxe horizontale du Soleil à une unité astronomique = 8.794148".
- le demi-diamètre solaire = 15´ 59.63".
- le rapport du rayon de Mercure sur le rayon équatorial terrestre : k = 0.3825096.
- le rayon équatorial terrestre = 6378140m.
- le carré de l'ellipticité de l'ellipsoïde terrestre = 0.00669438.
Pour le calcul des éphémérides de la planète Mercure et la Terre nous avons utilisé les théories suivantes :
- Les théories planétaires SLP98 sous forme de séries de polynômes de Tchebychev produites par G. Francou à partir des théories planétaires VSOP87 (P. Bretagnon et G. Francou, 1988).
- La théorie de la précession de Lieske (1976).
- La théorie de la nutation de Wahr (1981).
- La formule du calcul du temps sidéral d'Aoki (1992).
- Pour les époques anciennes, la différence entre le temps universel (UT) et le temps terrestre (TT) est calculée à l'aide des formules fournies par J. Chapront, M. Chapront et G. Francou (1997). Pour les époques futures cette différence est extrapolée à partir des dernières valeurs connues.
Pour chaque passage, on donne les informations suivantes :
- La date du maximum du passage.
- L'instant du maximum topocentrique en UTC.
- Le type de passage(P : partiel, C : central, NC : non central).
- La distance minimale topocentrique entre le centre du Soleil et le centre de la planète en minutes et secondes de degrés.
- La durée de la phase générale du passage.
- Puis pour chaque saros :
- Le numéro du saros de ce passage (un astérisque * après le numéro du saros désigne une série incomplète).
- Le numéro de ce passage dans ce saros.
VI. L'observation des passages de Mercure et Vénus devant le Soleil
L'observation de ces phénomènes nécessite l'observation
directe du Soleil, c'est donc une observation dangereuse. En résumé,
il faut, pour une observation à l'oeil nu, utiliser un filtre de
densité minimale 5 bloquant aussi bien le visible que les UV et
l'infrarouge (voir la page sur l'observation du Soleil
pendant une éclipse). Dans le cas d'un passage devant le Soleil,
la méthode fortement conseillée est celle de la projection
de l'image du Soleil sur un écran blanc: tous peuvent voir le passage
sans danger pour les yeux.
Pour observer le passage de Mercure ou de Vénus devant le Soleil,
il faut, bien sûr, que le Soleil soit visible aux instants prévus,
donc, tout simplement qu'il fasse jour. Enfin, la parallaxe fait que le
passage n'est pas vu sur la même partie du disque solaire selon le
lieu de l'observateur sur Terre. Ainsi, pour un passage rasant sur le bord
nord du disque solaire, il vaut mieux être dans l'hémisphère
nord : en vous déplaçant vers le sud, vous risquez de ne
plus voir de passage du tout... (c'est le cas du passage de Mercure le
15 novembre 1999 pour lequel certains observateurs de l'hémisphère
sud n'ont vu qu'une partie de Mercure devant le disque solaire). On
trouvera ici un lien vers une animation du passage de Mercure en conjonction
avec le Soleil, observé par le satellite SOHO.
accès aux prédictions des passages de Mercure devant le Soleil
accès aux prédictions des passages de Vénus devant le Soleil
accès à la prédiction du passage de Vénus devant le Soleil du 6 juin 2012