










 English
English
Comprendre > Concepts fondamentaux
Éclipses de Soleil
Chapitre 1. Généralités et définitions
- Quand ont lieu les éclipses de Soleil ?
- Les différents types d'éclipse de Soleil
- Durée maximum de la phase totale et de la phase annulaire
- Nombre d'éclipses par an
- Périodicité des éclipses, le Saros
- Les Canons d'éclipses
- La prédiction des éclipses de Soleil
- Fréquence des éclipses centrales de Soleil en France, dates des éclipses anciennes et futures
- Liste des éclipses de Soleil entre 1998 et 2020
1. Quand ont lieu les éclipses de Soleil ?
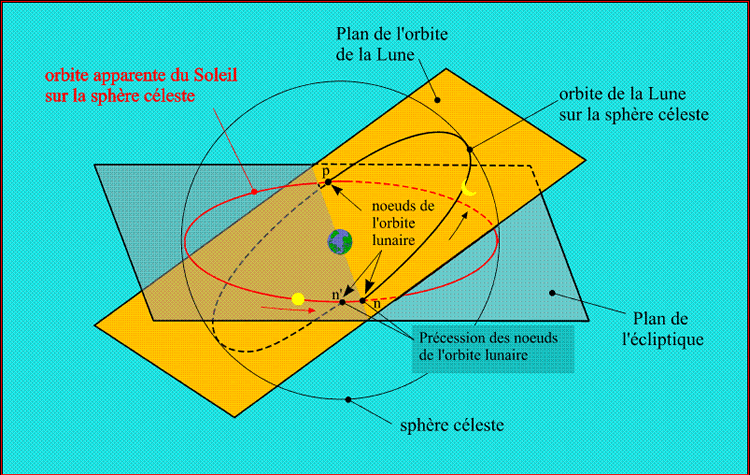
Il y a éclipse de Soleil lorsque la Terre passe dans le cône d'ombre ou dans le cône de pénombre de la Lune. Le Soleil, la Lune et la Terre sont alors presque alignés, et on est au voisinage de la nouvelle Lune. Si le plan de l'orbite de la Lune était le même que le plan de l'orbite de la Terre (écliptique), il y aurait une éclipse de Soleil à chaque nouvelle Lune, or le plan de l'orbite de la Lune est incliné d'environ 5° 9' sur le plan de l'orbite terrestre. À chaque instant, l'intersection de ces deux plans est une droite appelée ligne des noeuds et les intersections de cette droite avec l'orbite de la Terre sont appelées noeuds de l'orbite lunaire.
Cette ligne des noeuds n'est pas fixe, elle est animée, dans le sens rétrograde (sens des aiguilles d'une montre), d'un mouvement de précession d'une période de 18,6 ans (cf. §5), soit un déplacement de 19,354 8° par an.
Pour qu'il y ait une éclipse il faut donc,(dans le repère écliptique géocentrique), que la direction Terre-Soleil soit près de la ligne des noeuds lunaires au moment de la nouvelle Lune. Compte tenu du mouvement de précession des noeuds, le Soleil passe par un des deux noeuds tous les 173,31 jours. Cette période porte le nom de saison d'éclipses. Une éclipse de Soleil se produira si, au moment de la nouvelle Lune (instant où les longitudes géocentriques de la Lune et du Soleil sont égales, c'est-à-dire au moment de la conjonction en longitude), la latitude géocentrique apparente du centre de la Lune est inférieure à 1,42°, elle se produira peut-être si la latitude géocentrique apparente du centre de la Lune est comprise entre 1,42° et 1,58° et elle ne se produira pas si la latitude géocentrique apparente du centre de la Lune est supérieure à 1,58°.
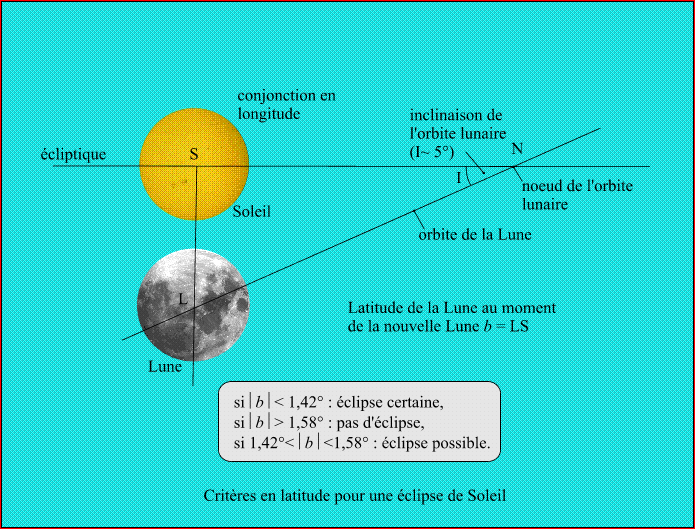
Ce critère sur la latitude du centre de la Lune, peut se traduire en un critère sur la longitude du Soleil. Ainsi il y aura éclipse si au moment de la conjonction en longitude, la différence de longitude entre le noeud de l'orbite lunaire et la longitude du Soleil est inférieure à 15,665°, il n'y aura pas d'éclipse si cette différence est supérieure à 17,375°, et il y aura peut-être éclipse si elle est comprise entre ces deux valeurs. Comme on le voit le critère en longitude est beaucoup plus large en amplitude que le critère en latitude, cela s'explique par la faible valeur de l'inclinaison de l'orbite lunaire.
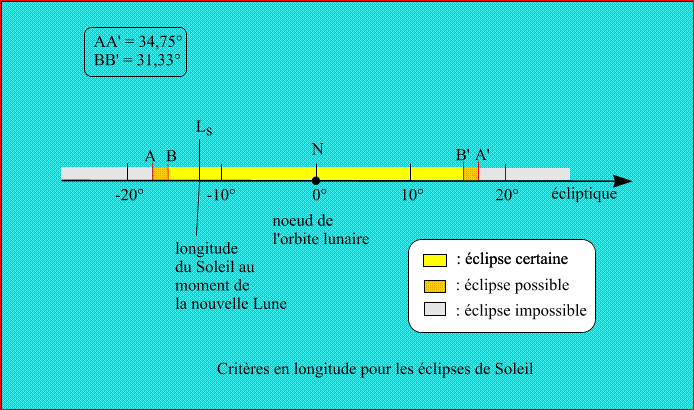
On peut faire au sujet de la figure 4 une remarque très importante, si la longitude du Soleil au moment de la conjonction se trouve sur le segment AB et qu'il n'y a pas d'éclipse, alors, compte tenu que la longitude du Soleil par rapport au noeud ne va varier que de 30,67° jusqu'à la prochaine conjonction, elle se trouvera sur le segment BB' et il y aura forcement une éclipse de Soleil. La valeur de cette variation de la longitude du Soleil par rapport au noeud (30,67°) en une lunaison reste inférieure à la longueur du segment BB' (31,33°); cela explique qu'il y ait toujours une éclipse de Soleil (et une éclipse de Lune) au voisinage de chaque passage du Soleil par l'un des noeuds de l'orbite lunaire.
2. Les différents types d'éclipse de Soleil
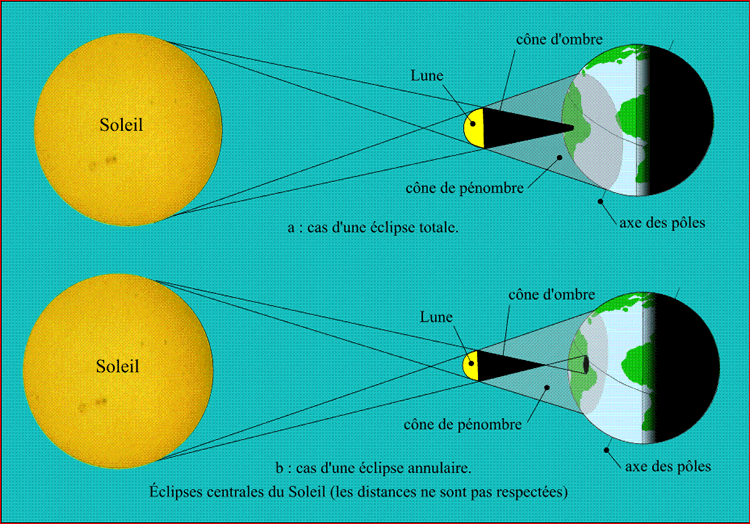
Les éclipses de Soleil se produisent donc à la nouvelle Lune, lorsque la Terre passe dans le cône d'ombre ou dans le cône de pénombre de la Lune (Fig. 5). Lorsque la Terre passe uniquement dans la pénombre de la Lune il y a éclipse partielle du Soleil, lorsque la Terre croise l'axe du cône d'ombre de la Lune il y a éclipse centrale du Soleil. La figure 5 se rapporte aux éclipses centrales, il y a deux types d'éclipses centrales : les éclipses totales, lorsque le diamètre apparent de la Lune est plus grand que le diamètre apparent du Soleil (le Soleil est complètement éclipsé), et les éclipses annulaires lorsque le diamètre de la Lune est plus petit que le diamètre apparent du Soleil. Il existe un cas limite lorsque le diamètre apparent de la Lune est inférieur au diamètre apparent du Soleil au début de l'éclipse, puis supérieur (autour du maximum) puis de nouveau inférieur au diamètre apparent du Soleil, dans ce cas l'éclipse est appelée éclipse totale-annulaire ou parfois éclipse de type mixte.
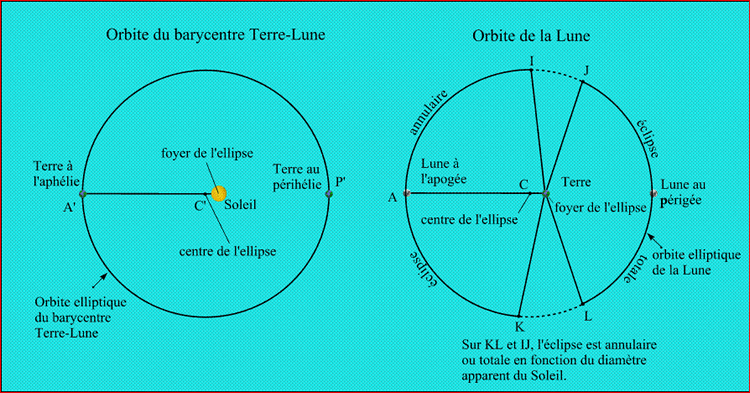
En raison des mouvements orbitaux de la Terre et de la Lune (Fig. 6), les distances Terre-Lune et Soleil-Terre ne sont pas constantes, les diamètres apparents de la Lune et du Soleil sont donc variables.

Cette figure montre les variations des diamètres apparents du Soleil et de la Lune en fonction de leur position sur leur orbite.
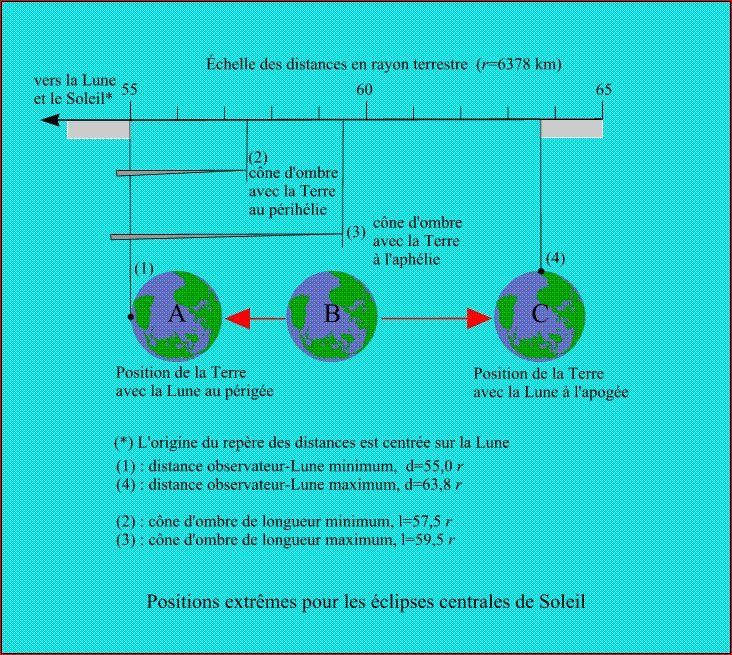
Cette figure donne les distances extrêmes de la Terre et du cône d'ombre, en fonction des positions extrêmes de la Lune, du Soleil et de la Terre. L'origine des distances est le centre de la Lune et les distances sont exprimées en rayon terrestre. La distance observateur-Lune varie de 55 à 63,8 rayons terrestres. La longueur de l'axe du cône d'ombre varie, elle, de 57 à 59,5 rayons terrestres. Cette figure nous montre que si , au moment de l'éclipse, on est dans la position A, c'est-à-dire avec la Lune au périgée, alors quelle que soit la position de la Terre sur son orbite, l'éclipse sera totale. De même si, au moment de l'éclipse, on est en position C, c'est-à-dire avec la Lune à son apogée, alors quelle que soit la position de la Terre sur son orbite l'éclipse sera annulaire. En faisant varier la position de la Terre (par rapport à la Lune) entre ces deux positions, on peut visualiser tous les cas intermédiaires possibles. Par exemple, lorsque la Terre est en B (distance Lune-Terre = 59 r), si la Terre est au périhélie (cône d'ombre en position 2) l'éclipse est annulaire, si la Terre est son l'aphélie (cône d'ombre en position 3) alors l'éclipse est totale, avec un cône d'ombre entre les positions 2 et 3 toutes les configurations sont possibles (éclipse totale, annulaire ou mixte).
Durant une éclipse, l'ombre et la pénombre se déplacent sur la surface du globe terrestre par suite du mouvement de la Lune et de la rotation terrestre. L'aire balayée par l'ombre, très étroite (quelques dizaines à quelques centaines de kilomètres), s'appelle la bande de centralité, la ligne parcourue par l'axe du cône d'ombre s'appelle la ligne de centralité, c'est sur cette ligne que se situe le maximum de l'éclipse. L'ombre se déplace sur cette ligne d'ouest en est; comme la Terre tourne également d'ouest en est, la vitesse de déplacement de l'ombre sur la surface du globe est égale à la différence des vitesses. Elle est de l'ordre de 3 380 km/h (939 m/s) près des pôles et de 1 706 km/h (474 m/s) à l'équateur.
Un observateur placé dans la bande de centralité voit d'abord une éclipse partielle puis, pendant un court instant (quelques minutes) une éclipse totale ou annulaire, puis de nouveau une éclipse partielle. L'aire balayée par la pénombre, à l'intérieur de laquelle l'éclipse est vue comme partielle, est beaucoup plus large (plusieurs milliers de kilomètres).
La durée maximum d'une éclipse générale (durée pendant laquelle l'éclairement de la Terre par le Soleil est altéré par l'ombre ou la pénombre de la Lune), c'est-à-dire le temps écoulé entre les deux contacts extérieurs du cône de pénombre, dépend de la vitesse de la Lune. Cette vitesse est maximale au périgée et minimale à l'apogée. Le calcul donne une durée maximum de 5 h 14 min pour une éclipse au périgée et une durée maximum de 6 h 15 min pour une éclipse à l'apogée.
3. Durée maximum de la phase totale et de la phase annulaire
Pour une éclipse totale
Une éclipse totale a une durée maximum lorsque l'ombre est la plus grande possible, c'est-à-dire lorsque la Terre est à l'aphélie, la Lune au périgée et lorsque le maximum a lieu au zénith du lieu d'observation. La première condition fixe la date de l'éclipse (actuellement début juillet). La troisième condition fixe le lieu d'observation sur le tropique du Cancer (latitude 23°). Avec la Lune au périgée, la vitesse synodique de l'ombre par rapport à la Terre est de 3 733 km/h (1 037 m/s) et la vitesse de l'ombre sur la surface de la Terre est de 2 196 km/h (610 m/s), son diamètre est alors de 262 km et la durée de l'éclipse est de 7 min 10 s. En réalité, ces paramètres ne sont pas indépendants et l'on s'aperçoit, en faisant un calcul plus rigoureux, que si l'on descend en latitude vers +5° la durée de l'éclipse croît jusqu'à 7 min 30 s. En effet le diamètre de l'ombre va décroître (on n'est plus au zénith, l'ombre devient elliptique) mais sa vitesse décroît encore plus rapidement ce qui en fin de compte augmente sensiblement la durée de l'éclipse. Le tableau suivant porte sur la totalité des éclipses comprises entre l'an -2003 et +2526 (réf. Canon of Solar Eclipses, 1983).
| Date | Durée | Date | Durée | Date | Durée |
|---|---|---|---|---|---|
| 22 juin -1460 | 7 min 04 s | 1 juin 132 | 7 min 14 s | 9 juin 1062 | 7 min 21 s |
| 3 juillet -1442 | 7 min 05 s | 12 juin 150 | 7 min 12 s | 20 juin 1080 | 7 min 18 s |
| 28 mai -1124 | 7 min 03 s | 23 juin 168 | 7 min 03 s | 1 juillet 1098 | 7 min 05 s |
| 9 juin -1106 | 7 min 02 s | 6 juin 327 | 7 min 04 s | 8 juin 1937 | 7 min 04 s |
| 24 mai -779 | 7 min 12 s | 16 juin 345 | 7 min 17 s | 20 juin 1955 | 7 min 08 s |
| 5 juin -761 | 7 min 26 s | 27 juin 363 | 7 min 24 s | 30 juin 1973 | 7 min 04 s |
| 15 juin -743 | 7 min 28 s | 8 juillet 381 | 7 min 22 s | 25 juin 2150 | 7 min 14 s |
| 26 juin -725 | 7 min 19 s | 19 juillet 399 | 7 min 11 s | 5 juillet 2168 | 7 min 26 s |
| 30 avril -443 | 7 min 01 s | 23 mai 681 | 7 min 10 s | 16 juillet 2186 | 7 min 29 s |
| 11 mai -425 | 7 min 12 s | 3 juin 699 | 7 min 16 s | 27 juillet 2204 | 7 min 22 s |
| 22 mai -407 | 7 min 13 s | 13 juin 717 | 7 min 15 s | 8 août 2222 | 7 min 06 s |
| 2 juin -389 | 7 min 04 s | 25 juin 735 | 7 min 02 s | 14 juin 2504 | 7 min 10 s |
| 22 mai 114 | 7 min 06 s | 29 mai 1044 | 7 min 12 s | 25 juin 2522 | 7 min 13 s |
Pour une éclipse annulaire
Dans le cas d'une éclipse annulaire le raisonnement est similaire mais inverse, le diamètre apparent du Soleil doit être le plus grand possible (Terre au périhélie) et le diamètre apparent de la Lune doit être le plus petit possible (Lune à l'apogée), dans ce cas le maximum peut atteindre 12 min 30 s. Le tableau suivant porte sur la totalité des éclipses comprises entre l'an -2003 et +2526 (réf. Canon of Solar Eclipses, 1983).
| Date | Durée | Date | Durée |
|---|---|---|---|
| 2 décembre -1673 | 12 min 02 s | 7 décembre 150 | 12 min 23 s |
| 12 décembre -1655 | 12 min 08 s | 17 décembre 168 | 12 min 15 s |
| 11 décembre -195 | 12 min 04 s | 25 décembre 1628 | 12 min 02 s |
| 22 décembre -177 | 12 min 08 s | 14 décembre 1955 | 12 min 09 s |
| 25 novembre 132 | 12 min 16 s | 24 décembre 1973 | 12 min 02 s |
4. Nombre d'éclipses par an
On peut calculer le nombre d'éclipses observables dans une année civile. Le Soleil, compte tenu du mouvement de précession des noeuds de l'orbite lunaire, passe par un noeud environ tous les 173,31 jours (cette valeur est connue sous le terme de saison d'éclipses). Les critères en longitude pour avoir une éclipse font que durant la lunaison voisine il y a obligatoirement deux éclipses, une de Lune et une de Soleil. On peut également avoir trois éclipses, soit deux de Lune et une de Soleil, soit deux de Soleil et une de Lune; alors l'éclipse unique est grande en magnitude (éclipse centrale de Soleil ou éclipse totale de Lune) et les deux autres éclipses sont faibles en magnitude (éclipses partielles pour le Soleil ou éclipses par la pénombre pour la Lune). Ainsi il y a une série d'éclipses toutes les six lunaisons. Donc si on tient compte de toutes les éclipses, y compris les éclipses de Lune par la pénombre, il y a au moins quatre éclipses par an, dont obligatoirement deux de Soleil et deux de Lune. Le nombre maximum d'éclipses par an est de sept, mais dans ce cas, il y aura encore obligatoirement au moins deux éclipses de Soleil et deux éclipses de Lune, pour les trois éclipses supplémentaires toutes les combinaisons sont possibles.
5. Périodicité des éclipses, le Saros
Lorsque la Lune et le Soleil sont au voisinage d'un des noeuds,
il y a éclipse de Soleil ou éclipse de Lune. La différence
entre la longitude moyenne de la Lune et celle du Soleil, est une fonction
linéaire du temps qui augmente de 360° en 29,530 5882 jours,
cette période « L » est appelée la révolution
synodique de la lune, ou mois lunaire ou bien encore lunaison.
Le plan de l'orbite de la Lune est animé d'un mouvement de précession;
ainsi les noeuds parcourent l'écliptique dans le sens rétrograde
(sens des aiguilles d'une montre). La période de ce mouvement des
noeuds est de 18.61 années
tropiques, soit 6 797,157 342 jours. La différence entre la
longitude moyenne de la Lune et celle du noeud ascendant de son orbite
est, comme la lunaison, une fonction linéaire du temps qui augmente
de 360° en 27,212 2208 jours, cette période « G »
est appelée révolution draconitique de la Lune. Pour
qu'il y ait retour des conditions favorables à une éclipse,
on doit donc trouver une relation entre cette période et la période
de la lunaison. On doit déterminer deux nombres x et y tel que x.G=y.L
ou encore x/y=L/G.
En utilisant la méthode de décomposition
des réels en fraction continue, on obtient entre autres :
x/y=1,085 196 = 242/223,
soit une période de 223 L, donc de 6 585,321 17 jours. Ce cycle, est connu sous le nom de Saros. Au cours de ce cycle, on retrouve en moyenne le même nombre d'éclipses. Mais les irrégularités du mouvement de l'orbite lunaire font que la succession du type des éclipses n'est pas conservée. Durant cette période, il y a en moyenne 84 éclipses (42 de Soleil et 42 de Lune), qui se répartissent, pour les éclipses de Soleil, de la façon suivante : 14 éclipses partielles et 28 éclipses centrales. Cette valeur de 84 éclipses est une valeur moyenne, en réalité on distingue des Saros pauvres, avec un petit nombre d'éclipses (78 éclipses), et des Saros riches avec un grand nombre d'éclipses (94 éclipses).
Cette période n'est pas un nombre exact de jours et la fraction de jour étant d'environ un tiers de jour, les éclipses se reproduisent bien le même jour mais avec un décalage en longitude d'environ 120 degrés.
À l'intérieur d'un Saros on peut observer des suites courtes d'éclipses de Soleil et de Lune. Elles portent sur huit ou neuf éclipses consécutives, réparties sur huit saisons d'éclipses. La grandeur de ces éclipses est croissante, jusqu'à la quatrième (ou la cinquième) éclipse, puis elle est décroissante.
On peut également mettre en évidence des suites longues d'éclipses en étudiant, non pas l'évolution des éclipses dans un même Saros, mais l'évolution des éclipses homologues d'un Saros à l'autre, c'est-à-dire celles qui surviennent à la même lunaison (numérotée de 1 à n dans les Saros successifs). On observe que sur une période de 72 Saros (environ 1300 ans), une éclipse de Soleil évolue de la manière suivante : une douzaine d'éclipses partielles de grandeur croissante, puis 48 éclipses centrales suivies de 12 éclipses partielles de grandeur décroissante. Ainsi des séries longues ont été construites par Van den Bergh (1955) à partir des 8000 éclipses du canon d'Oppolzer (cf. §6), chaque série longue, appelée parfois série de Saros est numérotée ainsi que chaque éclipse dans la série.
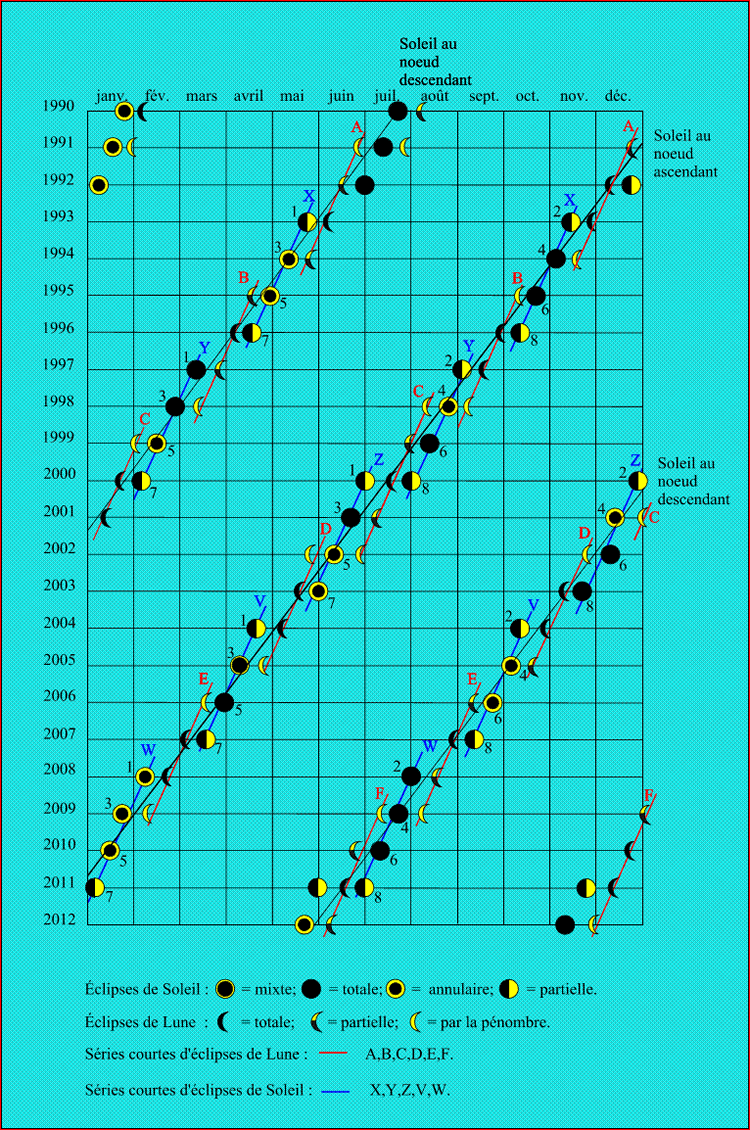
La figure 9 représente les éclipses sur 23 ans, de 1990 à 2012. On peut y observer par exemple un Saros allant de juin 1993 au premier juin 2011. Ce Saros contient 81 éclipses, dont 40 éclipses de Soleil et 41 éclipses de Lune, sur les 40 éclipses de Soleil, 15 sont partielles et 25 sont centrales (12 annulaires, 12 totales et une mixte) .
Cette figure met en évidence les nombreuses propriétés que nous avons déjà citées :
- la saison d'éclipses (corrélation entre les éclipses et les passages du Soleil aux noeuds de l'orbite lunaire),
- le fait qu'il y ait une éclipse de Lune et une éclipse de Soleil au moins chaque saison d'éclipses,
- les suites courtes d'éclipses de Lune et de Soleil (en rouge pour la Lune et en bleu pour le Soleil),
- le nombre minimum d'éclipses par an,
- lorsqu'il y a trois éclipses, l'éclipse centrale est maximum et les éclipses extrêmes sont des minima,
- les quatre dernières éclipses de l'année 2011 sont les homologues des éclipses de 1993, les quatre éclipses de 2012 sont les homologues de celles de l'année 1994.
6. Les canons d'éclipses
Les listes d'éclipses de Lune et de Soleil sont publiées dans des livres appelés canons d'éclipses. Le plus connu est celui de Theodor Ritter von Oppolzer, sa première édition date de 1887 dans le volume 52 des Mémoires de Mathématiques et de Sciences Naturelles de l'Académie Impériale de Vienne. Ce canon, corrigé, est réédité régulièrement par Dover Publications. Dans ce canon, on trouve 8000 éclipses de Soleil comprises entre -1207 et 2161 et 5200 éclipses de Lune comprises entre -1206 et 2132. Il faut préciser que l'on n'y trouve pas les éclipses de Lune par la pénombre.
Il convient de citer également le canon des éclipses
de Soleil de Jean Meeus et Hermann Mucke (1983, Astronomisches Büro,
Vienne), contenant toutes les éclipses de Soleil comprises entre
-2003 et +2526.
Ces deux canons ont été construits avec
des théories différentes des corps célestes et avec
des constantes légèrement différentes, cela implique
que certaines éclipses limites ne sont pas identiques (apparition
de nouvelles éclipses limites, ou éclipses totales dans un
canon qui deviennent mixtes dans l'autre).
7. La prédiction des éclipses de Soleil
Comme on l'a vu précédemment les éclipses de Soleil ont lieu au moment de la nouvelle Lune si le Soleil est près de la ligne des noeuds de l'orbite lunaire. Les valeurs moyennes de la lunaison et de la précession des noeuds de l'orbite lunaire sont connues depuis fort longtemps, les babyloniens les connaissaient déjà plusieurs siècles avant notre ère, alors pourquoi ne pouvaient-ils pas prédire les éclipses de Soleil ?
Cela provient du fait qu'il n'est pas possible de prédire une éclipse de Soleil à l'aide des mouvements moyens des corps concernés. En effet, un simple regard sur les éphémérides de la Lune, montre que les écarts entre deux nouvelles Lunes réelles et la valeur moyenne de la lunaison peuvent atteindre plus ou moins 7 h (cela est dû, entre autres aux variations de l'excentricité de l'orbite lunaire). La Lune peut se trouver 5,4° en avance ou en retard sur sa position moyenne, on peut faire la même constatation pour la position réelle du Soleil vu de la Terre, qui peut, elle aussi, se trouver 1,9° en avance ou en retard par rapport à sa position moyenne. Les diamètres apparents de ces corps étant de l'ordre du demi-degré d'arc, il est bien évidement impossible d'utiliser des valeurs moyennes, dont les écarts avec les positions réelles peuvent atteindre 15 fois le diamètre des corps, pour prédire une éclipse de Soleil. De plus la prédiction d'une éclipse de Soleil demande de déterminer sur quelle région de la Terre passe l'axe du cône d'ombre, donc de connaître avec précision les distances du Soleil et de la Lune à la Terre, ainsi que les dimensions de ces trois astres. Ainsi l'astronome babylonien, avec uniquement la connaissance des révolutions moyennes de la Lune et de la Terre, ne pouvait rien prévoir de plus que la possibilité ou l'impossibilité d'une éclipse de Soleil; il ne pouvait en aucun cas prédire si une éclipse serait ou ne serait pas visible en un lieu donné. En fait, aucun des textes chaldéens ou babyloniens connus de nos jours ne contient une quelconque référence à la période du Saros (ou à ses multiples) et c'est une erreur (hélas assez fréquente) de prétendre que les chaldéens ou les babyloniens la connaissaient.
Un passage de L'enquête d'Hérodote,
retraçant la guerre entre les mèdes et les lydiens, relate
qu'une bataille fut interrompue par une éclipse de Soleil et précise
que : « Thalès de Milet avait d'ailleurs prédit
cette éclipse aux Ioniens, pour l'année dans laquelle elle
se produisit ». Cette affirmation sera reprise par de nombreux
historiens, et elle deviendra la source d'une véritable légende
puisqu'à la prédiction d'une simple éclipse dans l'année
viendra s'ajouter celle de son jour et de sa position sur le globe terrestre,
chose tout à fait impossible pour un astronome de cette époque.
On peut s'étonner qu'il soit impossible de prédire
les éclipses de Soleil à l'aide des mouvements moyens de
la Lune et de la Terre, et que l'on puisse mettre en évidence la
périodicité des éclipses chaque Saros, le Saros étant
lui-même construit à l'aide des périodes moyennes.
Cela s'explique de la manière suivante : les écarts entre
les positions moyennes et les positions vraies sont dus aux mouvements
perturbés de la Lune et de la Terre, or la plus grosse perturbation
lunaire est fonction de la distance angulaire de la Lune au périgée
de son orbite, cet angle s'appelle l'anomalie. L'intervalle entre
deux passages de la Lune à son périgée s'appelle le
mois anomalistique et a pour valeur moyenne A=27,554 55 jours. Par
un heureux hasard on trouve que 239A=6 585,537 4. Le Saros est donc presque
un multiple du mois anomalistique (un Saros = 239A - 0,0079A), et au bout
d'un Saros la Lune moyenne se retrouve seulement 2,8° en amont de sa
position réelle. C'est cette coïncidence qui explique la régularité
du Saros. Pour la Terre, on peut faire un raisonnement analogue, il porte
alors sur l'année anomalistique qui à pour valeur
moyenne a=365,259 6 jours. On trouve que 18 a = 6 574,67 jours; l'écart
avec le Saros est de 10,65 jours, ce qui ne représente qu'un écart
de 10° environ avec la position orbitale réelle. Remarquons
de même, qu'au bout d'un Saros la position du Soleil vu de la Terre
sera environ 10° plus loin que sa position initiale; donc deux éclipses
homologues dans deux Saros consécutifs seront décalées
de 10° vers l'est parmi les constellations zodiacales.
8. Fréquence des éclipses centrales de Soleil en France, dates des éclipses anciennes et futures
Vu la faible surface traversée par la bande de centralité,
les éclipses visibles sur un territoire ayant la superficie de la
France sont peu nombreuses et si on se limite à une ville où
une région, elles deviennent exceptionnelles.
Le tableau suivant donne la liste des éclipses
dont la bande de centralité traverse la France, il porte sur toutes
les éclipses centrales allant du début du XVI
e siècle jusqu'à la fin du
XXI e siècle.
| Date | Type d'éclipses | Remarques |
|---|---|---|
| 24 janvier 1544 | totale* | visible dans le sud-est de la France |
| 12 octobre 1605 | totale | visible dans le sud-ouest de la France |
| 10 juin 1630 | totale* | la fin de l'éclipse est visible de l'ouest
au sud-est de la France |
| 27 janvier 1683 | annulaire | la fin de l'éclipse est visible
à l'ouest et au centre de la France |
| 12 mai 1706 | totale | visible dans le sud-est de la France |
| 22 mai 1724 | totale | visible du nord-ouest au nord-est de la France
visible à Paris |
| 1 avril 1764 | annulaire | visible dans le nord de la France
visible à Paris |
| 7 septembre 1820 | annulaire | visible dans le nord-est de la France
invisible à Paris |
| 8 juillet 1842 | totale | visible dans le sud-est de la France |
| 9 octobre 1847 | annulaire | visible du nord-ouest au centre-est de la France |
| 17 avril 1912 | mixte | visible de l'ouest au nord-est de la France
visible au nord de Paris (éclipse perlée) |
| 15 février 1961 | totale | visible dans le sud de la France |
| 11 août 1999 | totale | visible dans le nord de la France d'ouest en est |
| 5 novembre 2059 | annulaire | visible dans le sud-ouest de la France |
| 13 juillet 2075 | annulaire | visible en Corse et dans l'extrême sud-est de la France |
| 3 septembre 2081 | totale | visible dans le centre de la France |
| 27 février 2082 | annulaire | visible dans le sud de la France |
| 23 septembre 2090 | totale | fin de l'éclipse visible dans
le nord-ouest de la France |
(*) Ces deux éclipses sont données comme mixtes dans le canon de Meeus et comme totales dans le canon d'Oppolzer.
Remarque : quelques auteurs citent à tort l'éclipse du 12 août 2026 comme visible en France. Camille Flammarion la donne visible à Paris (1880, L' Astronomie Populaire). Paul Couderc la dit visible sur une ligne allant de Bordeaux-Toulouse (1971, Les éclipses). En réalité la phase de totalité de cette éclipse ne sera pas visible en France mais en Espagne.
Cartes des éclipses visibles en France :
Cliquez ci-après pour visualiser les cartes des bandes de centralité des éclipses du XVIème au XXIème siècles :
Éclipses des XVI, XVII et XVIIIèmes siècles.
Éclipses des XIX et XXèmes siècles.
9. Liste des éclipses de Soleil entre 1998 et 2020
On trouvera la prédiction des éclipses de Soleil pour les années à venir dans les pages "calculs astronomiques - éphémérides".
Crédit : P. Rocher/IMCCE