


 Français
Français
Understanding > Fundamental concepts > Celestial mechanics II
CELESTIAL MECHANICS
AND THE UNIVERSAL GRAVITATION
- The fundamental principle of dynamics
- The universal gravitation
- The 2-body problem
- Motions in the solar system
- The Lagrange points
- Comments on planetary theories
- The analytical theories
- The numerical integrations
- The time argument in the planetary theories
- Application : the eccentricity of the terrestrial orbit
The fundamental principle of dynamics
The fundamental principle of dynamics is a tool developed within the framework of classical mechanics, which allows to link the forces applied to a body and the kinematic evolution this body. Applied to a solid mass m , the motion of which being defined in a Galilean reference system, the principle states: F = mg = m dv / dt
F represents all the forces applied to the body and g is its acceleration.
Applied to a material point (a solid whose dimension is negligible compared to the distances) or to a group of material points, this law can be rewritten on various ways, all equivalent:
- the theorem of the motion of the center of mass (or barycenter)
"the barycenter of a material system moves as if
the entire mass of the system was there, the
external forces all acting on this barycenter";
-the theoreme of the cinetic moment applied
to a material point :
"the derivation relative to time of the cinetic moment
at a point of a material system is, at any time,
equal to the resulting moment of the external forces referred to
this point";
-the theorem of the cinetic energy :
"the variation of the cinetic energy of a material system
during a given interval of time is equal to
the sum of the work of internal and external forces
applied to the system during this time interval".
These principles are due to Huygens (1629-1695) and Galileo (1564-1642), but they have been improved latter by Clairaut (1713-1765), Descartes (1596-1650), Euler (1707-1783), D'Alembert (1717-1783), ...
Note that the theorem of the cinetic moment comes directly from the second Kepler's law (law of the areas), coming from the fact that the gravitational interaction is a "central" force.
The universal gravitation
The universal nature of gravity was identified by Newton (1642-1727) in his work "Mathematical Principles of Natural Philosophy". Newton was the first to realize that the apple falling from a tree and the Moon revolving around the Earth obey the same law and that their motionss are in fact similar.
The law of universal gravitation, one of the 4 fundamental interactions, reads as:
two material points of mass m and m' exert on each other an attractive force directly proportional to the masses and inversely proportional to the square of the distance r separating them. The module F of this force is :
F = G m m' / r2
where G is the constant of the gravitation.
This law requires the instantaneous transmission of forces in space. Celestial mechanics is then the application of Newtonian mechanics and of the fundamental principles of mechanics applied to the bodies of the solar system. from that, Laplace established the foundations of celestial mechanics.
The universal gravitation explains (almost) everything :
-the motions of planets and their satellites
-precession and nutation
-tides.
It does not explain the excess in the advance
of the perihelion of Mercury.
For explaining this point, it will be necessary to call the
theory of general relativity for which:
-there is no absolute time
-the notion of Galilean reference system is no longer
relevant
-the force-transmission is at the speed of light, and not instantly.
In a first approximation, Newtonian mechanics with
some additives explains perfectly the motions
in the solar system. But before describing this complex case,
it is primarily concerned to understand the problem restricted to two bodies.
The 2-body problem
The 2-body problem deals with two solid reduced to their center of mass, only to interact. This problem is analytically soluble, relatively simply, working in the center-of-mass system and the rest of the universe is forgotten, the center mass is isolated and provides a good Galilean reference system for the study of motion.
- First, we can show that the motion of one body around
the other is plane. This results from the fact that the angular momentum of
the system is constant, because the interaction is central, always
directed towards the barycenter of the system.
- Then, the gravitational interaction resulting in a "field of
force", it follows that the energy of the system
is also constant.
- Finally, the magnitude of the force evolving as the inverse of the square of
the distance between the two bodies, another invariant appears. This
invariant results into the eccentricity vector, and the path
of a body relative to another is like a
circle, ellipse, parabola or hyperbola. This trajectory,
in the plane of the motion is defined by its semi-major axis a and by its excentricity e.
Motions in the solar system
In the solar system we have the problem of N bodies interacting mutually.
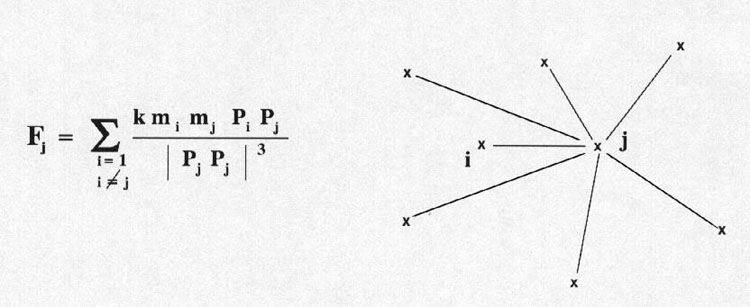
But if we look a little more closely, we realize that we have a very large body, the Sun, a thousand times more massive than the largest planets, Jupiter, surrounded by small bodies revolving around it. Each pair Sun-Earth is a 2-body problem. It can be considered as a first approximation that the mass m of the planet as negligible compared with that of the Sun (noted M) and the force applied to the planet is then :
F = -G Mm /r2
The coefficient GM, produced by the gravitational constant and by the
mass of the Sun, is the same for all planets,
that Kepler (1571-1630) has seen but has not demonstrated.
Lagrange points
For modeling motions in the solar system, we will start from the simplified problem in which trajectories of the planets are ellipses but whose elements of these ellipses will vary over time. This basic ellipse is called osculating ellipse. For each planet we will consider a two-body problem perturbed by other planets. It is Lagrange (1736-1813) during the XVIIIth century who solved the problem.
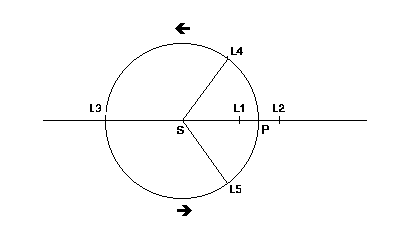
Lagrange also noted that in a two-body system, it exists equilibrium positions where an additional body could remain captive. These positions are called today Lagrange points of the two-body system. The figure below shows the location of the 5 points L1, L2, L3, L4, L5 (L1, L2 and L3 are also called "Euler points" since Euler detected them). Only L4 and L5 points are points of stable equilibrium. Asteroids are trapped on these points of the orbit of Jupiter and of Mars. Points L1 and L2 of the Earth are used to install telescopes for observation (Soho, a satellite observing the Sun at L1, Gaia, an astrometric satellite of observation and JWST for deep sky observation at L2). Points L1 and L2 are 1.5 million kilometers from the Earth. Attention, this system becomes unstable if the body has a mass P larger for more than 3% of the mass of the body S.
Comments on the planetary theories
The motion of the planets around the Sun is a special case of the N-body problem for which there is no exact solution for N greater than 2. All bodies attract each other according to the law of gravity but it is considered that the planets are small compared to the central body, the Sun. We search for approximate solutions of the problem based on the perturbation theory, where the coordinates are functions of time t, of the masses of the body in the presence and of integration constants. These solutions are obtained by constructing analytical theories or by performing numerical integrations.
The analytical theories
Coordinates are obtained as combinations of algebraic and trigonometric analytical functions of time t and of the parameters of the problem, masses and constants of integration. Calculating a position with such theories is long but relatively simple since just substituting the "time" parameter in series. Until the arrival of computers, it was necessary to build intermediate tables from which we could make ephemerides.
The numerical integrations
The numerical integrations provide numerical values for the coordinates and the velocities for times t0, t0+h, t0+2h, etc., t0 being the origin time and h the integration step. The methodes of numerical integration are well adapted toi calculations using computers. However, for calculating positions, it is necessary to build intermediate tables with the numerical integration and to make ephemerides using these tables.
The time argument in the planetary theories
It is useful to say a few words about the "time" argument of the ephemeris. Indeed, to find a position at a given time, what time should be used in the ephemeris? Until 1834, the true solar time of Paris was used. Then , due to the existence of more reliable clocks, the mean time of Paris was used. In 1916 , following an international convention, the mean Greenwich time was used. These time scales were previously associated with the rotation of the Earth considered as sufficiently uniform. The detection of irregularities in this rotation led astronomers to introduce an uniform time scale to calculate ephemerides, a time scale based on the rotation of the Earth around the Sun. The Ephemeris Time was defined from the theory of the Sun by Newcomb, or, as in the "Connaissance des temps", the uniform time of Le Verrier deduced from his theory of the Sun and therefore very similar to the previous of Newcomb. From 1984 was introduced the Terrestrial Time, an uniform time scale built from atomic clocks much more stable than the time scales deduced from the motion of celestial bodies.
Application : the eccentricity of the terrestrial orbit
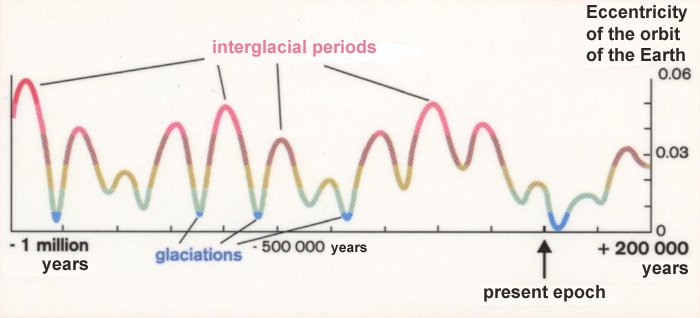
Celestial mechanics also provides, to a lower accuracy than for the ephemerides valid for several centuries, the evolution of planetary orbits over very long periods of the order of several million years. It is thus found that the eccentricity of Earth's orbit undergoes large variations formed of many periodic terms, the most important of which having periods of about 100 000 years, and for one of them, a period of 400,000 years. The works at the Institute of Celestial Mechanics (IMCCE in Paris), since the 1970s, have confirmed definitively the astronomical hypothesis of climate variations on Earth during the Quaternary Era. Paleoclimatologists indeed show the correlation between changes in the elements of the orbit of the Earth and major glaciations of the Quaternary. A circular orbit of the Earth corresponds to a glaciation and an elliptical orbit to a warmer period. The precision of the celestial mechanics clock provides to paleoclimatology the dates of glaciations and interglacial periods.
Credit : IMCCE



