


 Français
Français
Understanding > Fundamental concepts > Celestial mechanics III
GENERAL RELATIVITY
and Celestial Mechanics
In 1905 , A. Einstein (1879-1955) published his theory of restricted relativity, and in 1916, that of general relativity. The theory of gravitation of Newton has reached its limits. Some phenomena are not explained and it will need to find a better model. But what implications will have these new theories in the dynamics describing the solar system? Will these new theories help us to understand better what is gravitation? Before discussing the innovations introduced by these new theories let us come back a little on the theory of gravitation of Newton and on celestial mechanics which was built on its foundations.
Newton's gravitation
The universal gravitation is a fundamental discovery of the eighteenth century. All motions of the solar system appear to be explained and the discovery of Neptune by Le Verrier will devote celestial mechanics built on these foundations.
Let's remind Newton's law:
F = -Gmm'/r2
where F is the force exerted on each other by two respective bodies of masses m and m ' separated by a distance r. G is called the constant of gravitation.
On the other hand , the inertia principle discovered by Galileo provides that a body which moves without external interaction, will continue indefinitely on a straight path. Newton added that the only way to change this trajectory is to use a force: an object undergoing a force accelerates inversely proportional to the mass of the object in the direction of the force quantity.
Newton's theory also explains the flattening of the Earth and can correctly describe the tides. It was well thought before that the Moon could draw water seas but then, the tide would have being higher only on the side of the Moon. Newton explained: the Earth revolves around the Sun, it is not in a Galilean reference and undergoes the attraction of the Moon. Nothing keeps the Earth fixed as the water rises to the Moon. Differential forces clearly explains the high tides on both sides of the Earth. Finally universal gravitation does not only apply to the solar system but the entire universe.
Dynamics , gravitation and celestial mechanics allow us to describe motions in the solar system, but in fact, they do not explain anything. We are in the presence of an action at distance. Why bodies attract themselves? Nobody knows. Before Newton, it was believed that angels pushed the planets in their orbits, but after Newton, we know that angels do not push planets but to draw the planets to the central body to counteract the principle of inertia! No mechanism has been identified to explain the action of this force.
The gravitational constant
In the Newton formula above, we see the existence of a constant G. What is it ? What is its value? In fact , the measurement of distances and periods in the solar system gives us the product Gm of the constant G with the mass of the central body. So we know G x (solar mass) by measuring the positions of planets , G x (Earth mass) by measuring the motion of the Moon , G x (mass of Jupiter) by measuring the positions of Jupiter's satellites, etc.. The first measurement of G was made by Cavendish (1731-1810) in 1798. For this he made a now famous experiment: it measures the attraction of two lead balls of 150 kg each on small ball via a torsion pendulum. He can say: I weighed the Earth! The conventional value of this constant is
6,672 59 x 10-11 m3 kg-1 s-2 (accuracy superabundant because beyond 6,672 decimals are not very significant...). This determination allows us to know the mass of bodies in the solar system and solve problems such as:
- what would be the rotation period of a ball of negligible mass around a mass of one kilogram put at one meter located in space without any perturbation? Applying Kepler's 3rd
law of Kepler n2 a3 = GM i.e. a3/T2=GM/4π2
where a =1 m, M =1 kg, we have : T2 = 4π2/G
= 4π2/6,672 59 x 10-11
= 5,91663 x 1011 seconds2 then T = 7.692
x 105 seconds = 8 days 21 hours et and minutes.
A question also arises: is the gravitational constant really constant or does it change over time? It was impossible to measure a variation of this constant but this variation, if it exists, is very small. Indeed, assuming that this constant has varied from 10% in the last billion years, the Sun's radiation conditions were such that life on Earth would have been impossible at that time. The variation of this constant may be much lower than this. Position measurements of the Moon through laser shots give us a variation of G such that G'/G<10-12/an
The principles of relativity
After considering the nature of gravity, we come to the principle of relativity. This principle is not new. From the very beginning of mechanics, the question to be asked is: do the laws of physics remain invariant in any reference frame? Does an absolute reference frame exist? This is the fundamental question that theories of relativity will try to answer.
The Galilean relativity
Even before the discovery of universal gravitation by Newton, Galileo states the principle of inertia: any body left to itself and undergoing no external force is driven by a uniform rectilinear motion. Be called "Galilean reference" reference systems in which this principle is verified. These systems are in uniform rectilinear translational motion relative to each other. To switch from a Galilean reference frame to another having a velocity v parallel to the x-axis, the change of variable is of the form:
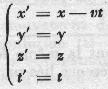
In this transformation called " Galilean " laws of mechanics and physics are assumed to be invariant. Speeds are cumulative. To respect the principle of inertia , Newton will have to introduce an absolute time and a universal absolute space.
This simple system will live for more than one century and celestial mechanics described wonderfully dynamics of the solar system until two grains of sand slip into the machine. One will be the excess of the advance of the perihelion of Mercury. Unexplained residual discovered by Le Verrier in 1859 and confirmed by Newcomb in 1895 is the first serious challenge to the theory of Newton. Classical mechanics is powerless against this problem. The other is of a different kind: it comes from the discovery of electromagnetism where action at a distance gives way to a physical field, an action of contact. In 1873 , J. Maxwell (1831-1879), a Scottish physicist, publishes general equations of the electromagnetic field , known as " Maxwell's equations ". It becomes apparent that these equations are not invariant. Indeed, the composition of the velocities does not work with the speed of light which does not depend on the speed of the source (it should be observable when observing double stars) and can not be added with another speed. Could it be due to the existence of an "ether" in which light travels by vibration? One then tried to detect a motion relative to the ether. In particular, it should be able to measure the speed of a mobile by measuring variations of the speed of light due to the wind of ether. It was then the famous experiment performed by Michelson in 1881 of measuring the difference in speed of light in two perpendicular directions. This experiment was made in various places , 6 months apart (the speed of the Earth changes its direction) for decades and found no significant change in the speed of light (recent experiments with modern means tested the isotropy of the propagation of light around 10-13). The motion of the Earth was undetectable with this method. Maxwell's equations were they wrong ? Actually no, it was the Galilean transformation which was not correct. H. Poincaré showed that Maxwell's equations were invariant if they apply a particular transformation , called "Lorentz transformation".
Einstein's restricted relativity
Einstein will succeed in extending the principle of relativity from mechanics to physics from two assumptions, the first being due to Lorentz and Poincaré:
- all Galilean frames are equivalent for the formulation of physical laws;;
- the speed of light in vacuum is constant with respect to any Galilean system and is independent of the motion of the source and the direction of propagation.
These two assumptions are of course incompatible with the Galilean transformation which postulates that there is an absolute time and the measurement of length is independent of the motion of the reference system. Einstein will show the errors of these assumptions. In particular, it shows the relativity of the concept of simultaneity which has meaning only within a given Galilean system, resulting relativity of the concept of length. Length and time are related. Galilean transformation is, as expected, to be replaced by the Lorentz transformation:
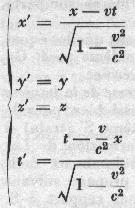
for two inertial reference systems R and R' having their axes parallel and with the relative motion of velocity v along the x axis.
The law of composition of velocities is no longer that of the Galilean system.
This transformation will lead length contraction and expansion of durations for moving bodies. Note that for small relative velocities compared to c (ie v/c small), the Lorentz transformation is reduced to the Galileo transformation.
Let us clarify these notions of length contraction and time expansion: the length of an object at rest in R will be seen in R' with the length L' = L square root (1-v2/c2) < L (thus length contraction). Now consider two events A and B occurring at the same point R separated by a time interval T. The time T' measured between these two events in R' will not be T but T '= T /square root(1-v2/c2) > T (thus time expansion).
Relativistic dynamics
The laws of the Newtonian dynamics are also changing: they must be invariant in a Lorentz transformation.
The fundamental law F = d/dt(mv) where m and v vary upon time .
The momentum p = mv becomes:
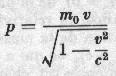
In the Newtonian mechanics, the notion of mass has two meanings: its detection through its weight (gravitational mass) and its detection by its resistance to motion (inertial mass). These masses are proportional, and the units are chosen so that they are identical. By identifying the above expression with p=m(v), we deduce that:
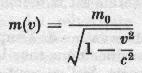
where m0 is the mass at rest.
Einstein's relativity thus introduced the concept of mass at rest and induces an increase in mass with velocity.
The total energy of a moving body becomes:
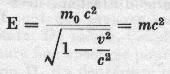
i.e. by developing :
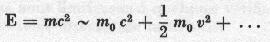
Einstein's theory introduces a new term:
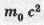
which corresponds to the "internal energy" in addition to kinetic energy and thus there is equivalence between mass and energy.
All these developments have been verified by the particle physics allowing very high speeds. At low speeds, we come back to the laws of the Newtonian dynamics.
The general relativity
Restricted relativity has not solved all the problems. It has been unable to incorporate gravitation satisfactorily and some experiments always seem to prove that there is an absolute reference. For example, the experience of the Foucault pendulum suggests that we can measure the motion of the Earth relative to an absolute reference. So where is the contradiction? For that, Einstein will extend the restricted relativity to gravitation and Einstein will state the principle of equivalence. The identity between gravitational mass and inertial mass is a basic premise of the theory. Thus, it is not possible locally to distinguish an acceleration force from a force created by the gravity. This identity has led Einstein to believe that a laboratory in free fall in a gravitational field constitute somehow the natural extension of the concept of inertial reference system of the old mechanics. We are thus led to postulate that "all systems of reference in free fall are equivalent for the expression of non-gravitational laws of physics, regardless of their state of motion and location." This statement constitute what is now called the Einstein equivalence principle.
It should be noted here that this principle does not impose anything on the description of gravitational phenomena themselves. Thus, it does not postulate that two laboratories in freefall located in different places will find the same value for the gravitational constant G (being admitted they are equipped with clocks and meters the same production). In other words, the Einstein equivalence principle does not reject a priori that the "real relativistic theory of gravitation" can predict that G varies with time and place. This principle allows generalizations of general relativity, generalizations the tests of which are the subject of much current research.
The idea that in the presence of a gravitational field, it is the reference frames in free fall that will replace the inertial frames ,leads very naturally into another : reference frames in free fall can only be local, because a true gravitational field (that of the Earth, for example) is not uniform. Indeed, the non-uniformity causes that no overall motion of the reference system can not remove all the field of the Earth. Hence the idea that the Einstein equivalence principle, which is purely local, does not prohibit the geometry of space-time to change from one point to another. On the contrary, such a change in geometry solves the problem of gravitation with an extreme conceptual elegance. The Galilean principle of inertia says that in the absence of any force field, a material point has a rectilinear uniform motion in any inertial frame. However, a straight line is a geodesic of the Euclidean space. It is therefore natural to consider the motion of a particle in free fall in a gravitational field as defined by a geodesic of a more complex metric than the Euclidean metric. In fact, Einstein introduced a generalization called "pseudo- Riemannian" of the space-time metric of the restricted relativity.
We give below an analogy that helps to understand why a non-Euclidean metric can account a simple force of gravity .
 .
.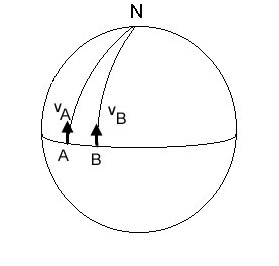 .
. We can therefore describe gravitation as a manifestation of the curvature of a metric.
Experimental evidences of general relativity
The list of experimental tests of general relativity is very long and we cite below the most significant:
- excess of the advance of the perihelion of Mercury determined from observations and unexplained in the Newtonian system coincides with the effect predicted by general relativity;
- the bending of light rays passing near a mass is detected by observing the stars near the Sun during an eclipse and it is in good agreement with general relativity ;
- gravitational mirages (lens effect of a large mass in the path of light rays) were observed (see below) ;
- the motion of the Moon observed with great precision thanks to laser shots is in excellent agreement with the theory of general relativity;
- slower orbital period detected in the binary pulsar PSR 1913 +16 is easily explained by the emission of gravitational radiation provided by general relativity;
- the expansion of the universe discovered by Hubble through the redshift of distant galaxies can be explained by Newtonian cosmology but the observations are best explained by general relativity on very large distances.

Crédit : J.E. Arlot/IMCCE



