


 Français
Français
Understanding > Fundamental concepts > Seasons
THE SEASONS
- Definition of seasons
- The orbit of the Earth around the Sun
- The rotation of the Earth and the Earth's equator
- The line of the equinoxes and the line of solstices
- The length of days and nights
- The dates of the seasons
- The tropical revolution
- Why do seasons always fall on the same dates ?
- Calendars used in the calculation program
- The drift of the seasons in the Julian calendar
- Season dates in the Gregorian calendar
- The duration of the different seasons
- Some historical considerations
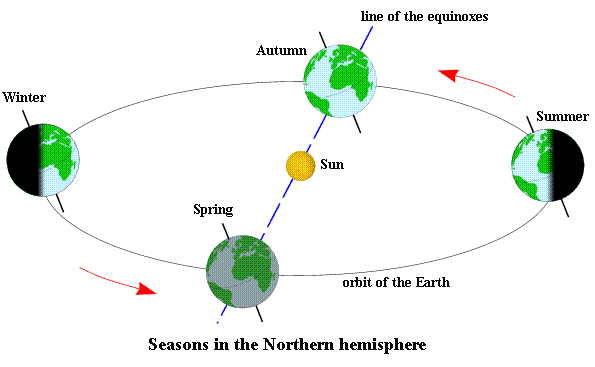
1. Definition of the seasons
1.1. The orbit of the Earth around the Sun
As a first approximation , the center of gravity of the Earth- Moon system runs in the forward direction (counter clockwise) , on an almost flat and elliptical orbit around the Sun (according to Kepler's first law) . The plane of the orbit is called the Ecliptic plane . The Sun is located at one of the focus of the ellipse. The eccentricity of the ellipse is so small as to be undetectable, the orbit being close to a circle. It is important to note that the Sun is not the center of the ellipse , but at one of these focus. The distance between the Earth-Moon barycenter and the Sun is not constant. There are two particular positions corresponding to the extreme values of the distance: perihelion ( minimum distance ) and aphelion ( maximum distance ) . The line joining these two positions is called line of apsides .
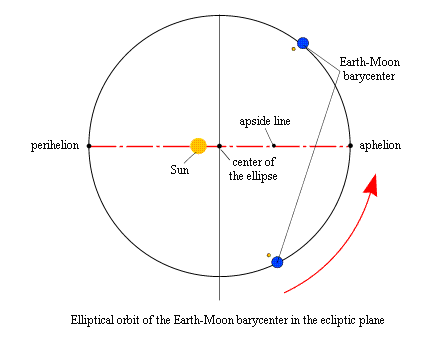
1.2. The rotation of the Earth and the Earth's equator
The Earth rotates around its polar axis in the forward direction ( west to east ) . The axis of rotation of the Earth is not perpendicular to the plane of the orbit of the Earth-Moon barycenter ( the Ecliptic ) . This tilt, 23 degrees 26 minutes , is at the origin of changes in the length of days and nights and seasons. The plane normal to the axis of rotation of the Earth cutting the terrestrial sphere into two hemispheres is called the Earth equatorial plane. The intersection of this plane with the Earth is the Earth's equator.
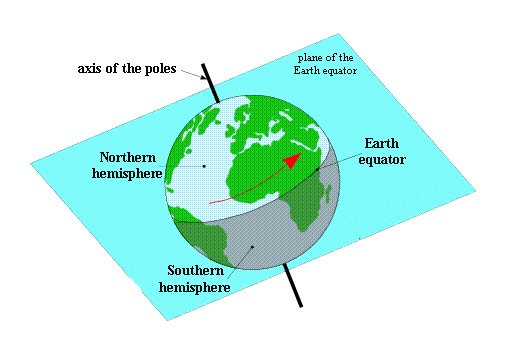
1.3. The line of the equinoxes and the line of solstices
As the axis of rotation of the Earth is not perpendicular to the plane of the ecliptic, the Earth equatorial plane is not parallel to the plane of the ecliptic. So it cuts it along a straight line . This line is called the line of the equinoxes. When the direction of the line joining the Sun to the Earth is parallel to this line , the Earth is at the equinoxes.
There is another specific line, the line perpendicular in the plane of the ecliptic to the equinoxes line. This line is the line of solstices. When the direction of the line joining the Sun to the Earth is parallel to this line , the Earth is at the solstices.
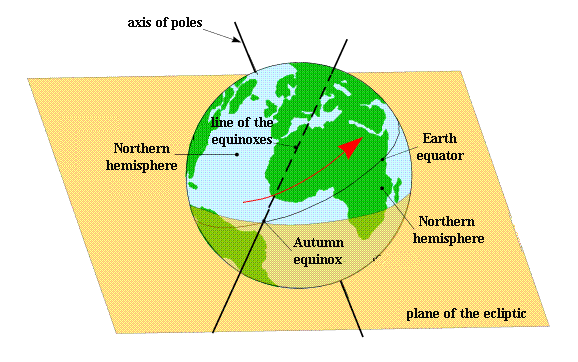
Seen from Earth , in the geocentric equatorial frame, the equinox corresponding to the passage of the Sun from negative to positive declinations is called spring equinox (beginning of spring in the northern hemisphere) or vernal point . This direction is, in the plane of the ecliptic, the origin of celestial longitudes and is also, in the plane of the equator, the origin of right ascensions.
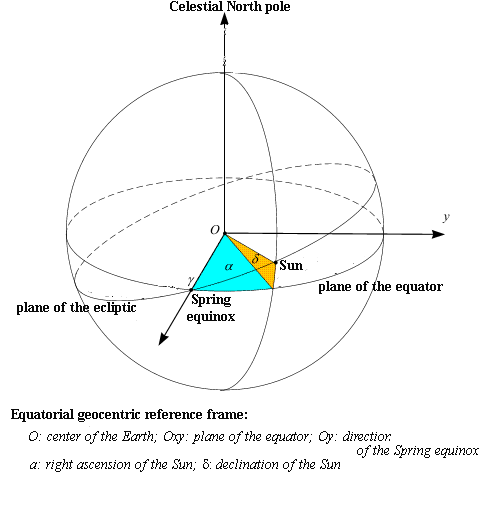
The spring in the northern hemisphere corresponds to the time when the apparent geocentric longitude of the center of the Sun is equal to 0°. The other equinox, corresponding to the passage of the Sun from positive to negative declinations, is called the autumnal equinox (the beginning of autumn in the northern hemisphere). Autumn in the northern hemisphere corresponds to the time when the apparent geocentric longitude of the center of the Sun is equal to 180°.
The solstice between the spring equinox and the autumnal equinox is the summer solstice and the solstice between the autumnal equinox and the vernal equinox is the winter solstice. Summer in the northern hemisphere corresponds to the time when the apparent geocentric longitude of the center of the Sun is 90°. Similarly, the winter solstice in the northern hemisphere, is the moment when the apparent geocentric longitude of the center of the Sun is equal to 270°.
1.4. The length of days and nights
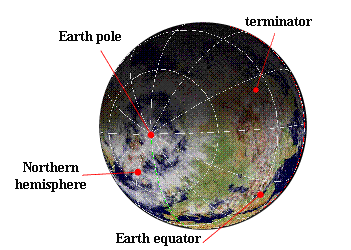
The day of the equinox (spring or autumn), the terminator of the night zone on the Earth passes through the Earth's poles. The day of the equinox, when the atmospheric refraction is neglected, the day length is equal to the duration of the night everywhere of the Earth's surface. On the day of the equinox, the Sun rises East and sets exactly in the West.
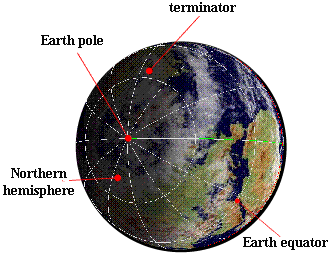
The day of the winter solstice , in the northern hemisphere , the half-sphere defined by the terminator of the night zone covers most of the surface of the northern hemisphere. This is the day of the year when the length of the night is maximum and the length of day minimum. This is also the day when the Sun rises over the south-east , passes the meridian with a minimum height and sets the most south-west.
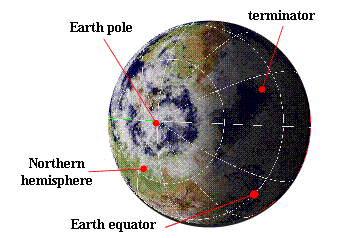
The day of the summer solstice in the northern hemisphere , the half-sphere defined by the terminator of the night zone covers the smallest part of the surface of the northern hemisphere. This is the day of the year when the length of the night is the minimum and the duration of the day maximum. This is also the day when the Sun rises over the north-east , passes the meridian with a maximum height and sets the most north-west.
The following figure shows the apparent paths of the Sun for specific days for a place in the northern hemisphere.
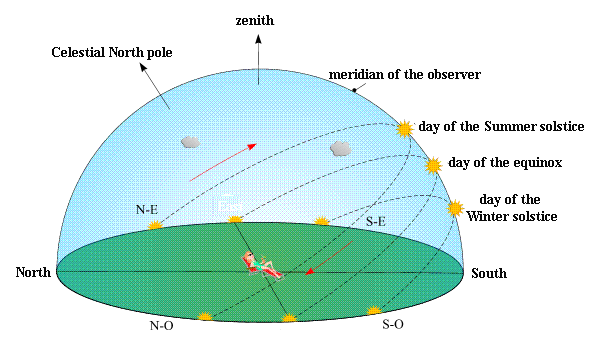
In the southern hemisphere, the solstices and equinoxes are the opposite of the solstices and equinoxes in the northern hemisphere.
See the pages on the rises and sets for more details on the length of days and nights.
2. The dates of the seasons
2.1. The tropical revolution
The time interval between two consecutive passages of the Earth in the direction of the vernal equinox is called the tropical year . Its average value is 365.2422 days ( or 365 days 5h 48m 46s ). This period is less than the sidereal year , which corresponds to the time interval between two passages of the Earth in the same direction and is equal to 365.2566 days ( or 365 days 6h 9m 10s) . This is because the direction of the equinox is not fixed . It is driven by a precessing motion in the retrograde direction (50.2877 " per year) . This movement called precession is related to the movement of the axis of rotation of the Earth , which describes a cone in the retrograde direction in about 26 000 years.
2.2. Why do seasons always fall on the same dates ?
This is due to our calendar , the Gregorian calendar , which is built to have an average length the nearest to the tropical revolution of the Earth. As the tropical revolution is not a whole number of days, if it takes a calendar year of 365 days, there is a shift of 0.2422 days from one year to another in the date of the seasons and, after four years , this shift is almost one day. To compensate for this, it was, at first, added a day to the year every four years (leap year of 366 days). This was the Julian calendar developed by Julius Caesar in 46 BC.
But if one day every four years is added , the average value of the calendar year is 365.25 days. It is a bit too high compared to the tropical year . So if you just add a leap year every four years, the seasons will shift slowly from the calendar of 0.0078 days per year ( 11min 14s per year). Thus, the Julian calendar follows badly the seasons . It shifts about 3 days after 400 years.
To get a better match between the calendar and the seasons, simply remove three days over a period of 400 years.
This is what is done in the Gregorian calendar. As in the Julian calendar, leap year is added every four years (those being a multiple of four) except for years that are multiples of 100 without being 400. Thus 1600 and 2000 are leap years, but 1700, 1800 , 1900 and 2100 are not leap years.
This reform of the calendar was made by the Pope Gregory XIII in 1582. In addition, to remove the accumulated shift between seasons and the old calendar (Julian calendar ) and to bring the date of the vernal equinox on March 21 , the year 1582 has been shortened by 10 days, the next day after Thursday October 4, 1582 becoming Friday, October 15, 1582.
2.3. Calendars used in the calculation program
The calculation program of season dates gives these dates in the Julian calendar for dates prior to October 5, 1582 and in the Gregorian calendar for the post- October 15, 1582 dates. The Julian calendar was extended for dates prior to the beginning of the Christian era using the notation of astronomers and not the historians' one.
2.4. The drift of the seasons in the Julian calendar
As we saw in a previous paragraph, the dates of the seasons shift in the Julian calendar about three days every 400 years . We can see this drift with the calculation program of the season dates.
| Year | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|
| 0 | 22 March | 24 June | 25 September | 22 December |
| -1000 | 30 March | 2 July | 2 October | 29 December |
| -2000 | 7 April | 10 July | 9 October | 6 January |
| -3000 | 14 April | 18 July | 15 October | 13 January |
| -4000 | 22 April | 25 July | 22 October | 20 January |
Shifts of the dates of the seasons in the Julian calendar
2.5. Season dates in the Gregorian calendar
As we saw it, the Gregorian calendar was built to prevent the shift of season dates that we found in the Julian calendar . Season dates are always near to the same dates in the Gregorian calendar . The use of leap years makes an oscillation of three and exceptionnaly four days the date of the seasons.
The dates of the vernal equinox (spring)
During the nineteenth and twentieth centuries , the vernal equinox always falls on 20 or 21 March. In the past it has fallen on March 19 in 1652 , 1656 , 1660 , 1664 , 1668 , 1672 , 1676 , 1680 , 1684 , 1685 , 1688 , 1689, 1692, 1693, 1696 , 1697 , 1780 , 1784 , 1788 , 1792 and 1796. It will again fall on March 19 in 2044.
The dates of the summer solstice
In the Gregorian calendar , the summer solstice may fall on 19, 20 , 21 or 22 June. In general, it falls on June 21: it fell on June 20 in 1896 and fell back on that date in 2008. It fell on June 22 in 1975 and will fall back on this date in 2203 , 2207 , 2211 and 2215 and in 2302. The summer solstice falls on June 19 in 2488 (and this is the first time since the creation of the Gregorian calendar) and in 2492 and 2496.
The dates of the autumn equinox
In the Gregorian calendar , the autumnal equinox may fall on 21 , 22, 23 or 24 September. It generally falls on 22 or 23 September . It will fall on September 21 in 2092 and this is the first time since the creation of the Gregorian calendar. It will happen again in 2096 , then 2464 , 2468, 2472 , 2476 , 2480 , 2484 , 2488 , 2492 , 2493 , 2496 and 2497. It fell on September 24 in 1803 , 1807 , 1903 , 1907 , 1911 , 1915 , 1919 , 1923 , 1927 and 1931 , it will fall back to that date in 2303.
The dates of the winter solstice
In the Gregorian calendar, the winter solstice may fall on 20 , 21, 22 or 23 December. It generally falls on 21 or 22 December. It fell on December 23 in 1903 and will fall back on this date in 2303 , 2307 , 2311 and 2315. It fell on December 20 in 1664 , 1668 , 1672 , 1676 , 1680 , 1684 , 1688 , 1692 , 1696 and 1697 and will again fall on this date in 2080 , 2084 , 2088 , 2092, 2096 , 2488 , 2492 and 2496.
3. The duration of the different seasons
3.1. The length of seasons
Just looking to a calendar to check that the lengths of the different seasons are not equal . For example in 1998, the winter lasted 89 days , the spring 92 days 18 hours , the summer 93 days 15 hours and autumn 89 days 21 hours .
This change in the length of the seasons is due to the fact that the speed of the Earth-Moon barycenter in its orbit around the Sun is not uniform. This is an immediate consequence of the second law of Kepler. The orbital velocity is not constant . So when the Earth-Moon barycenter is closer to the Sun (at its perihelion ) its speed is maximum and when the Earth-Moon barycenter is farthest from the Sun (at its aphelion ) the speed is minimal. But nowadays the Earth-Moon barycenter passes at perihelion in early January and at aphelion in early July. So the Earth is faster in its orbit in January and winter is the shortest season; same, the Earth is slowest in July and summer is the longest season.
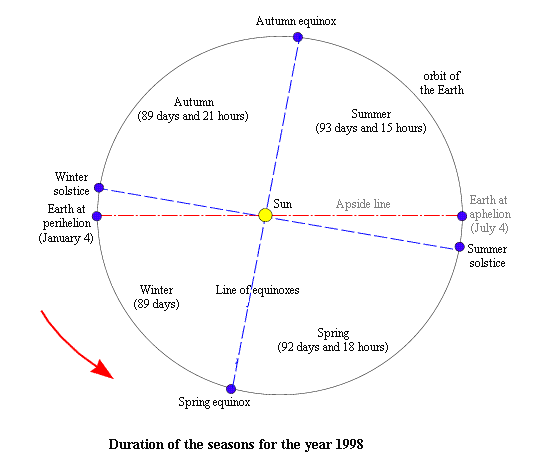
This figure shows that the season is not a function of the distance between the Sun and Earth. Currently , in the northern hemisphere , the coldest season (winter) is the time when the Sun is the closest to the Earth and the hottest season (summer) is the time the Sun is farthest from the Earth.
3.2. The evolution of the length of seasons
If the positions of the perihelion and aphelion of the Earth-Moon barycenter were constant over time , the duration of the different seasons would be , too, constant. But the orbit of the Earth-Moon barycenter turns in its plane in the forward direction at about 12 " per year ( one revolution in about 100 000 years .) The precession occurs in the opposite direction ( retrograde ) at a rate of 50.2877 " per year ( one revolution in about 26 000 years). The combination of these two movements is used to calculate when the perihelion of the Earth will be in the direction of the vernal equinox: this period of about 21 000 years is called the climate precession. Indeed, all 10 500 years ( half-period of climatic precession ) aphelion moves from summer to winter . But even if the Earth-Sun distance is not the dominant factor in the nature of the seasons , the combination with the passage of the Earth at aphelion in winter gives hardest winters.
4. Some historical considerations
4.1. The precession of the equinoxes and the length of the tropical year
The name of Hipparchus of Nicaea (ca. 190 - approx. 125 BC ) is linked to the discovery of the precession of the equinoxes. To discover the slow motion of the line of the equinoxes, two observation methods are possible. The first is to measure changes in the longitudes of the stars over time. This method is cumulative , as each year the longitude increases from a low but constant value. The second method is to measure the gap between the tropical year and the sidereal year . We know from Ptolemy ( second century AD) that Hipparchus used these two methods. And this is probably the first method which was responsible for the discovery of the precession of the equinoxes. For this he compared the distance of Spica in the Ear of the Virgin ( alpha Virginis stars ) with the autumnal equinox the dates of Timocharis' observations , observations made between 294 and 283 BC and the value of that distance in his time. He found a variation in the longitude of the star of 2 degrees over the period of 160 years between the two measures.
To determine the values of the tropical year and the sidereal year , Hipparchus used initially observations made between 162 and 128 BC, but the values calculated from these observations seem to indicate a variable value of the tropical year with time . Finally, he was limited tohis own observations of the solstices that he had made himself in 135 BC, to the observations made by Aristarchus in 280 BC and to the observations made by Meton in 432 BC. For the tropical year he found a value of 365 days plus a quarter and minus 1/ 300 of a day (or 365 days 5h 55m 12s) and for the sidereal year , he found a value of 365 days plus a quarter plus 1/ 144 of a day (or 365 days 6h 10m 0s ) . These values are quite close to current values.
The following table lists the various values of the tropical year as a function of the epoch of determination.
| Epoch | Author | Value |
|---|---|---|
| 141-127 BC | Hipparchus | 365d 5h 55m 12s |
| 45 BC | Julius Caesar (Sosigene) | 365d 5h 55m |
| 139 AD | Ptolemy | 365d 5h 55m 12s |
| 499 | Aryabhata | 365d 8h 36m 30s |
| 882 | al-Battani | 365d 5h 48m 24s |
| ~1100 | Khayam | 365d 5h 49m 12s |
| 1252 | Alphonsines Tables | 365d 5h 49m 16s |
| ~1440 | Ulug Beg | 365d 5h 49m 15s |
| 1543 | Copernicus | 365d 5h 49m 29s |
| 1574-1575 | Danti | 365d 48m |
| 1582 | Gregorian Calendar | 365d 48m 20s |
| 1986 | Laskar | 365d 5h 48m 45.187s |
In fact the value of the tropical year is not constant but varies slowly with time , its value is given for a given time by the following equation (J. Laskar , 1986) :
A =3 65,242 189 669 8 - 0,000 006 153 59 T - 7,29 x 10 -10
T 2 + 2,64 x 10 -10 T 3
where T = (JJD - 2 451 545,0) / 36 525
JJD being the Julian day of the considered date.
4.2. The length of seasons
The Papyrus of Eudoxus informs us that Callipe (around 370-330 BC.) was one of the first astronomers to accurately determine the length of the different seasons. He found (94, 92 , 89 and 90 days) from the vernal equinox . Hipparchus improved the values found (94 1/2 , 92 1/2 , 88 1/8 and 90 1/8) always from the spring equinox . Note that these values are very different from current values and this is normal. Indeed, if we take into account the climatic precession , the angle between the perihelion and the spring equinox was at the time of Hipparchus 34 degrees greater than at the present time. The perihelion was thus falling in autumn and aphelion in spring , and the shortest season was actually the fall season and the longest season, the spring.
click here to get the dates of the seasons for any year
Credit : IMCCE



