


 Français
Français
Understanding > Fundamental concepts > Calendars III
Determination of Easter date
Date of Easter. - The importance of the date of Easter in the civil life is that, in France as in many countries, some mobile Christian feasts are occasions of holidays: Easter Monday, Pentecost Monday (50 days after Easter), Ascension (ten days before Pentecost).
This date was subject to a definition of astronomical nature in the year 325 when the Council of Nicaea adopted the following rule yet accepted in a large part of the Roman Empire:Easter is celebrated on the Sunday following the fourteenth day of the Moon reaching this age on 21 March or immediately after. In this definition , the term "age of the Moon" is not taken in its usual sense: age is counted in whole days, from the day of the New Moon(1), day on which it receives the value 1.
In fact, the date of the New Moon, which is used for the application of the rule of Nicaea is not extracted from astronomical tables, or obtained by direct observation of the crescent (practice still in use for observation of some Muslim holidays). It is taken in a lunar calendar, the Julian or Gregorian, as appropriate, established once and for all, the distribution of the New Moons being made empirically, with an average interval based on knowledge of this time on mean motions of the Moon and the Sun.
The search for the date of Easter is therefore not an astronomical problem, and the only rational method to use is to use tables attached to this page or, of course, using the interactive computing proposed at the end.
The calculations leading to these tables represent the computus. Lunations defined by the two lunar calendars are lunations (Julian or Gregorian) of computus. The lunation of the computus that contains Easter is the Paschal Moon.
By construction, the Easter date can not be before March 22: it is positioned so if the Paschal moon starts on March 8, and if March 22 is a Sunday.
The latest date is April 25. Indeed, in the Gregorian computus, a lunation m(of 29 days) can begin on March 7 and the fourteenth day being March 20, the Paschal moon is the next one, which begins on April 5; if April 18 falls on a Sunday, Easter falls on the next Sunday. In the Julian computus, it is the same as if there is no possible New Moon on March 7, a lunation can start on March 6, and it is then that lasts 30 days.
The Gregorian lunar calendar is in agreement with the mean motion of the Moon , but as a result of inequalities of this movement and discontinuity in the values of the lunation of the computus (29 or 30 whole days), a difference of 1 or 2 days is possible between the astronomical New Moon and New Moon Gregorian. However, according to the fourteenth day of the Moon is 20 or 21 March, the date of Easter is later or earlier by a lunation, so this date may be in error by 29, 30 or even 31 days relatively to the date to be obtained by the use of astronomical ephemeris.
According to a popular belief, it is stated that the date of Easter Catholic (or Protestant, it is the same), or the date of Orthodox Easter is delayed in order to avoid coinciding with the date of Jewish Passover. It is not true but the thing sometimes occurred during the first centuries. Indeed, the coincidence of the two feasts was to the pagan philosophers subject of derision against the two religions, who claimed to be opposed and which seemed to follow the same liturgy to celebrate the events (exodus of the Hebrews and resurrection of Christ) which are independent, but the second occurred in the week of Passover. At the Council of Nicaea, a controversy arose first: "Some argued that it should follow the custom of the Jews, others claimed it was necessary to examine the exact time, and do not agree with a people so far away from the grace of Scripture" (Eusebius(2), Life of Constantine , III, 5). A third solution prevailed : eliminate any risk of coincidence through the Nicaea rule, Passover being fixed as follows: it occurs the fourteenth day of the lunation of spring (or, if that day was a Friday, to the day after, i.e. Saturday). Unfortunately, the Jews did not use the fictitious Moon of the Christian computus, (but nowadays a Moon substantially near the astronomical Moon), so that the desired effect was not reached. It has now no more object.
The Nicaea rule is not part of the dogma, and any Ecumenical Council could change the rule when the interest will be sufficiently felt. Any changes have been explicitly proposed in the acts of the council of 325 and finally the rule itself was not enacted at the time by the Pope, but by the Emperor Constantine, who was baptisted only on his deathbed, 10 years later.
Elements of the computus. - The Julian computus uses two elements, the Dominical letter and the Golden number. The Gregorian computus uses the Dominical letter and theEpact, but the knowledge of the Golden number is also necessary, contrary to what is usually said. The solar cycle is an element whose employment is equivalent to the Julian Dominical letter. The fifth element, theRoman indiction, has no role in the current computus; it served in an ancient Christian chronology, based on a division of time into successive cycles of 15 years from the year 313 of the Christian era, and in which it indicated the rank of a year in its cycle.
The value of these elements is given each year in the almanacs, so it is publish in the Connaissance des Temps and in theAnnuaire du Bureau des longitudes. Because of this publication, theAnnuaire du Bureau des longitudes devoted to the computus a periodic article, which naturally concluded by calculating the date of Easter, the text of this article was also very much the reproduction of the late book IV of the 3rd edition Cours d'astronomie de H. Andoyer de 1923. This is an unjustified tradition: the elements of the computus have no scientific role, civil, or even religious, they have been used in the past to establish the date of Easter. The tables below give the value for a period before the end of which that Easter will certainly become, if not fixed, at least not very mobile, and finally their use to find the day of the week corresponding to a given date, especially for the reverse operation is more complicated than using the perpetual calendar published here and yearly in the Annuaire du Bureau des longitudes-Ephémérides astronomiques.
Dominical letter and perpetual calendar. - We make a correspondance between the letters A, B, C, D, E, F, G and each day of the year, beginning with January 1, A, and the cycle repeating every seven days. If the year is common, this is done once, and ends with A for December 31. If the year is a leap year, the operation is performed in two steps: until 29 February, which is D, and from March 1, which is also assigned the letter D. The letter corresponding to any day (defined by the month and day number) of the year is the same in both cases.
A day of the week is assigned with the same letter throughout a common year, the Dominical letter is the letter assigned to Sundays. In a leap year, two letters are assigned to Sundays, one in the first two months, the other in the last ten and the second is before the first in the alphabetical order (or is G if the first is A): the Dominical letter is then double. In the Gregorian calendar, Dominical letters for 1974, 1976, 1984 are respectively F, DC, AG.
The tables in annex give the Dominical letter in the Julian and Gregorian calendars. In the first, the Dominical letter comes back after 28 years (first whole integer number of years always containing an integer number of weeks); the first multiple of 28 and 100 is 700, then the layout of the table. In the Gregorian calendar, the 28-year period ceases to be valid when the regularity of the sequence of leap years suffered an interruption (what happens in 1700, 1800, 1900, 2100...), but it appears that 4 centuries, exact period of this calendar, contain an exact number of weeks the Dominical letter thus reproduces at this range.
The knowledge of the Dominical letter of a year allows to find the day of the week corresponding to a given date, so to establish a perpetual calendar. Table I provides for each date the letter that corresponds to that date, according to the rule given at the beginning of this paragraph. In Table II, we find the column corresponding to the year in question, thanks to the Dominical letter, topping the column; on the table row containing the letter obtained by Table I in this column, we read at top, the name of the searched day.
If the year is a leap year, the Dominical letter consists of two letters, the first of which being suitable for the first two months, the second for the other months.
TABLE I
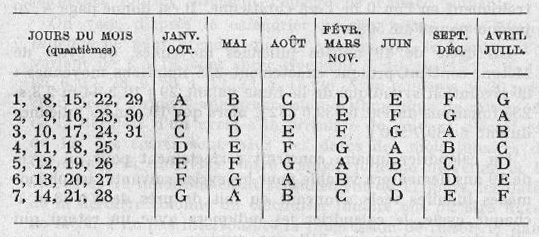
TABLE II

Solar cycle. - The Solar cycle is the rank of a year in the cycle of 28 years in a time scale made of such cycles, and arbitrarily starting in the year 20 of the Christian era.
In the Julian calendar, as we have seen, the days of the week can be found on the same dates at the end of 28 years, mainly Sundays consecrated in the past to the Sun, that this is the origin of the name given to the cycle.
The knowledge of the solar cycle, whose values are given in annex, is equivalent to the Julian Dominical letter. There is a perpetual calendar based on the solar cycle valid in the Julian calendar, and having the same role as the perpetual calendar based on the Dominical letter.
Golden number and Julian perpetual calendar. - The Golden number is the rank of a year in the 19-year cycle of a time scale made of such cycles and arbitrarily starting in year 0 of the Christian era. It is given below in Annex until the year 5099.
A cycle of 19 mean Julian yeras, or Metonic cycle, contains almost exactly 235 mean lunations: the synodic revolution of the Moon being 29 days 12h 44m 2.8s, 235 lunations last 6 939.6 882days, while 19 Julian years last 6 939.7500 days.
A lunar calendar built correctly for a 19-year cycle will remain valid for the next cycles; the real lunar phenomena are advancing around 1h 30min each cycle, so the timing of the calendar will have a delay of one day after 310 years.
The perpetual Julian lunar calendar dates back to the sixth century. It sets, in a 19-year cycle, the dates of the Julian New Moons, which are distributed fairly regularly with a little deviation from the astronomical New Moons when there is an agreement at the beginning of a cycle. It includes 115 lunar months of 29 days and 130 of 30 days, alternating substantially, totaling 19 times 365 days.
If the year is a leap year, it is by convention the lunar month containing the 24 February which is extended by one day; if this month does not contain the 29 February, the beginning of the next lunar month will be back of one day from the normal date.
The lunar calendar is on the following page in annex. It gives the dates of the Julian New Moons according to the Golden number; the three dates in February put in brackets are specific to leap years, as it has been said. Dates in italics correspond to the beginning of the lunar month of 30 days.
Epact. - The age of the Moon is, exactly, the time elapsed since the time of the last New Moon, measured in days. In the following, it is the integer part of this value, measured at midnight of that day, which will be named age of the Moon for this day; the age ranges from 0 to 29, with 0 corresponding to the calendar day of the New Moon.
The epact of a year is the age of the Moon on 1 January of this year; this is not the Moon itself, but the fictional object defined by the computus. The date of a New Moon in December, noted in the tables of the perpetual lunar calendar provides easily the epact of the next year.
We see from the Julian lunar calendar, that the Julian epact can take only 19 values which, the Golden number ranging from 1 to 19, are successively 8, 19, 0, 11, 22, 3, 14, 25, 6, 17, 28, 9, 20, 1, 12, 23, 4, 15, 26. To a multiple of 30, these values form an arithmetic progression of ratio 11; from the last of the first cycle to the first of the next cycle, the difference is 12. These differences come from the dates of the lunar month of December, the average difference between the Julian year and the value of 12 lunar months being substantially 11 days, the dates of the last column of the lunar calendar could be fixed in order to avoid to stop the progression of reason 11 in the succession of the epacts of the same cycle.
In 1582, the Gregorian reform has removed 10 calendar days in advance, so the dates of the lunar calendar therefore drop 10. In addition, the error of the Metonic cycle giving to the Julian Moon a delay on the Moon Astronomical up to 3 days (1 day for three centuries since the sixth century), a second correction of value of 3, was to be introduced. The julian epact being 3 in 1582, theGregorian Epact took the value 3-10 +3 + (30) = 26.
From that date, the Gregorian epact follows the law governing the Julian epact with two corrections: first to each non-leap centennial year, it should be sustract one day to the epact: it is the Solar equation of the epact, and second, to compensate the error of the Metonic cycle, correcting the epact by +1 at intervals leading to an average correction of one day in 310 years, i.e. seven times after three centuries and once after four: this is the Lunar equation of the epact, which was implemented in 1800 and will be in 2100.
The difference between the two epacts was 23 until 1699, 22 from 1700 to 1899; it is 21 now, and remained 21 until 2199 as solar and lunar equations for 2100 will compensate. After correction, and until the next one, the Gregorian epacts form a suite of cycles of 19 integer values included between 0 and 29 in arithmetic progression of reason 11 (to a multiple of 30); from a cycle to another, the epact increases of 12. The cycles coincide with those of the Julian epacts. Thus, from the value 26 for the year 1582, the epacts are 7, 18, ..., 27, 8, 19 until 1595; the year 1596, that have a golden number of 1, begins a Julian cycle and the Gregorian epact takes the value 19 +12- (30) = 1. The cycle of Gregorian epacts for the period 1582-1699 is the series of 19 numbers 1, 12, 23, 4, 15, 26, 7, 8 ... 18, 19.
Gregorian epacts are given in the pages in annex. For the Epact 25, see the next paragraph.
Perpetual Gregorian lunar Calendar. - The calendar is built from the Julian lunar calendar, the Gregorian New Moons are tabulated according to the epact, which takes all values from 0 to 29. It takes into account the shifts introduced by the non Julian epacts.
To improve the regularity of the succession of the New Moons of the computus, it was made a few transfers between the months of 29 and of 30 days. Were especially created the epact 25bis or 25, which is to be used in place of the epact 25 if the golden number is greater than 11. The discontinuity of +1 in the progression of the epact is still continuing after the Golden number reached the value 19 , but this value occurs here for any line of the calendar: the New Moon of December of the 19th line of the calendar should be delayed by a day, which resulted in a redistribution of the dates of this line; on the other hand, all the months of December, when the Golden number will be found to be 19, will have 29 days instead 30.
The Perpetual Gregorian Lunar calendar is given in the pages in annex. As for the Julian calendar, the dates in italics are the beginnings of lunar months of 30 days and dates in parentheses are specific to leap years. The dates in brackets of December are those suitable for cases where the Golden number is 19; the epact 25 is to be used when the epact is 25 and the Golden number is larger than 11.
Determining the date of Easter for a given year. - In the table of the Julian lunar calendar, each line defined by the Golden number of the considered year, makes it easy to find the Paschal moon, which begins in March, after the 7th or in April before the 6th ; we deduce the date of the 14th day of the Paschal moon. The day of the week for that date will be obtained by the universal calendar from the Dominical letter of the year. Easter of the Julian calendar is the Sunday following that day.
These operations are avoided using directly the Julian Easter table, which is their equivalent and which has as argument the Golden number and the Dominical letter.
In the table of the Gregorian lunar calendar, the same procedure as above was carried out, but according to the Gregorian epact. If it is 25, the Easter moon begins on April 5 if the Golden number does not exceed 11, and on April 4, otherwise (epact 25). This gives the date of Easter in the Gregorian calendar.
These operations are avoided using directly the Gregorian Easter table, which is their equivalent and whose arguments are the Gregorian epact and the Dominical letter. The knowledge of the Golden number would be required if the epact was issued from the calculation and was 25 (see previous paragraph).
All these determinations are pure exercises, because the date of the Easter sunday, in the Julian and Gregorian calendars, is given as a function of the year in the tables in annex. The Julian table extends at will to the past or the future: the Dominical letter and the Golden number respectively having a period of 28 and 19 years, the Easter Sunday is found on the same day of the year after 28 x 19 years = 532 years. The Gregorian table given here until the year 3000, does not extend as for the Julian table.
Formulas. - The elements of the computus and the date of Easter can be put under mathematical formulas such as those listed below; they are given only as a curiosity since the tables are not issued from them. The demonstration of these formulas requires only elementary arithmetic knowledge that does not mean it is always easy, and Gauss, the creator of the first formulas, had himself committed an error in the expression of the Gregorian epact, which happened to be incorrect for years after 4199.


DATE OF EASTER SUNDAY in the Julian calendar
In the Julian calendar, Easter periodically returns to the same dates after an interval of 532 years, cycle named Paschal cycle
, a specific feature which can extend to any Julian year the dates provided by the table below.
Example. - When Easter fell in the year 870? Adding to 870 two Paschal cycles, i.e. 532 x 2 = 1064, we obtain 1934 which, in the next page, 8th line , fifth column, gives the number 26. In the year 870, the date of Easter was on March 26.
In the tables that will be obtained by clicking on the proposed links, dates in italics correspond to the month of March and those in bold face to April.
Dates of Easter Sunday in the Julian calendar 1600-1859
Dates of Easter Sunday in the Julian calendar 1860-2200
Dates of Easter Sunday in the Gregorian calendar 1583-1949
Dates of Easter Sunday in the Gregorian calendar 1950-2319
Dates of Easter Sunday in the Gregorian calendar 2320-2689
Dates of Easter Sunday in the Gregorian calendar 2690-3000
SOLAR CYCLE AND JULIAN DOMINICAL LETTER since year zero until the year 5599
GREGORIAN DOMINICAL LETTER from 15 October 1582 until the year 5099
GOLDEN NUMBER since year zero until the year 5099
Gregorian EPACT since 15 October 1582 until the year 3299
Gregorian EPACT since 3300 until the year 5099
JULIAN LUNAR CALENDAR PERPETUAL
GREGORIAN LUNAR CALENDAR PERPETUAL
JULIAN PASCHAL TABLE
GREGORIAN PASCHAL TABLE
BIBLIOGRAPHIC REFERENCES
Annuaire du Bureau des longitudes pour 1971, p. 407-431.
H. ANDOYER, Cours d'astronomie, 1ère partie : Astronomie
théorique, 3ème éd., Paris, 1923, p. 434-447.
P. COUDERC, Le Calendrier, P.U.F., Paris 1961.
M. MONTUCCLA, Histoire des Mathématiques, t.I, Paris,
1758, p. 581-598.
J.M. OUDIN, Étude sur la date de Pâques, Bulletin astronomique,
XII, 8, Paris, 1946, p. 391-410.
Note (1) : In the spirit of ancient texts, the day of the New Moon is the day after the night in which it was possible to discern the appearance of the first crescent.
Note (2) : Eusebius, bishop of Caesarea (not to be confused with the pope in the same time and with the same name), is the father of Julian lunar calendar; he proposed to the Council its construction based on the Metonic cycle and obtained satisfaction with difficulty.
Credit : J. Lévy/Annuaire du Bureau des longitudes



