


 Français
Français
Understanding > Fundamental concepts > Time I
ROTATION AND REVOLUTION OF THE EARTH :
TIME SCALES
Definition of the day
True solar time, mean solar time
The time scales
Precession and nutation
Definition of the year
The rotation of the Earth around its axis defines the day and the revolution of the Earth around the Sun defines the year.
To fully define the motion of the Earth, we need to know:
- The motion of the axis of the Earth referred to the "outside" (that is to say with respect to an inertial reference frame): it is this motion that defines the motion of the celestial equator and the modification of the coordinates (precession
and nutation);
- The motion of the axis of rotation of the Earth relative to the Earth itself (polar motion): it is very small since the pole remains in a circle of about twenty meters, but this motion is unpredictable;
- The motion of the Earth around its axis of rotation is obviously the most important that will define the notion of day. It is expressed by the evolution of an angle: the sidereal time.
Definition of the day
If we consider a fixed direction in space, it will take 23h 56m 4s for an observer to find it in the same direction after a complete revolution of the Earth around its axis. But this is not really noticeable. It will be more visible if the Sun returns to the same position. It is this return of the Sun in the same direction that defines the average day lasting about 24 hours.
The day is not , a priori, a single unit of time to count durations , but rather a time period centered on a "day" and framed by periods of "night" . We will define the day as the time between two successive passages of the Sun at its highest point , that is to say, the " meridian " of the site . But such a duration is variable and we will see why.
First, as we shall see later (Kepler's laws), the apparent orbit of the Sun around the Earth (actually, the real orbit of the Earth around the Sun) is not a circle but an ellipse and the apparent velocity of the Sun on the celestial sphere will vary according to its position on its trajectory. Therefore the Sun will pass at the meridian ahead when it goes faster or late when it slows down, compared to an average position. In order to have hours regularly distributed and to avaoid twelve o'clock coming a little early or a little late depending on the date, a theoretical average position of the Sun that defines the mean solar time , a time scale that has been in use until the early 1970. The official definition of this time scale was as follows:" the legal time in France is the mean solar time of Paris delayed by 9m 21s and increased by 12 hours (this is the definition of Universal Time internationally recognized) and also increased by one hour in summer and two hours in winter (it is summer time or winter time). The 9m 21s are used to put us in the hour of international meridian (Greenwich) and the twelve hours in advance are added to make more convenient starting the day at midnight instead of noon (the average mean solar time starts the day at noon when the Sun passes the meridian) and finally the shift of one hour or two hours gives us the summer time or winter time . Time zones are there to allow a similar shift for countries located far from the international meridian in order to have the Sun at its highest point near noon.
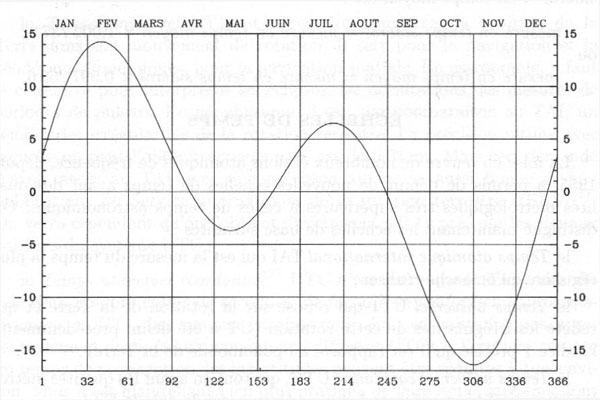
True solar time , mean solar time , equation of time
True solar time at a place and at a given moment , is the hour angle of the Sun in this place at this time. It is provided by sundials. It is , of course, affected by the irregularities of the rotation of the Earth and is connected to the mean solar time by the relation: true solar time = mean solar time minus equation of time.
It is this difference between the mean Sun and the true Sun -i.e. the equation of time- that makes us saying in January : "hey , the days lengthen more in the evening than in the morning" .In fact, it is the true noon that moves and happens later compared to the average noon. This difference between the average noon and the true noon is obviously fundamental when building a sundial providing only the true time of the place where it is built. This difference is called the " equation of time " . It reaches a maximum of 16 minutes late October.
True solar time = mean solar time - Equation of Time
The equation of time is actually the result of two effects :
- The equation of the center due to the eccentricity of Earth's orbit (the path of the elliptical and not circular orbit of the Earth)
- The reduction at the equator due to the obliquity of the ecliptic (the Earth does not rotate around the Sun in the equatorial plane) since the passage of the Sun is measured at the meridian of the place relative to the Earth equatorial plane in which it is necessary to bring it back.
Thus, the equation of time gives the number of minutes after or before twelve o'clock to go back to the true noon. Example: If the equation of time is equal to 8 minutes , then it will be true noon at 12pm 8m mean time .
More simply , the Earth rotates around its axis in the plane of the equator and around the Sun in the plane of the ecliptic. It is the advance (or late) of the Sun, referred to an uniform motion in the ecliptic , which must be projected on the equator.
You may have a look to the pages on the sets and rises of celestial bodies for more details on the length of days and nights.

The image above shows the effect of the equation of time . Images of the Sun taken 10 days in 10 days in the morning at the same time were superimposed.
The time scales
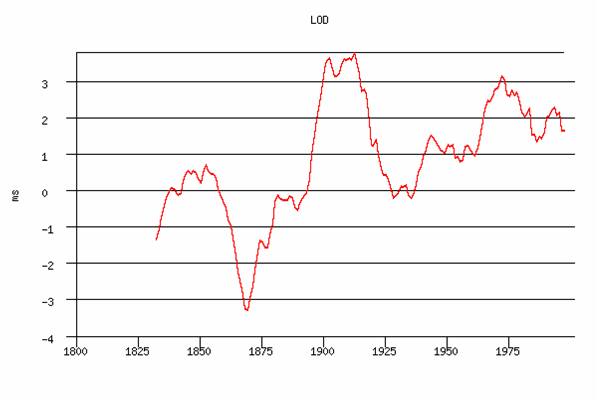
The diurnal rotation of the Earth around its axis has long seemed sufficiently uniform to provide a basis for the time scale used by astronomers and called Universal Time (UT). In this time scale, the second is defined as equal to 1/86400 of the mean solar day. But it was discovered that the Earth was slowing, seeing that the Moon was escaping from the Earth in a way that was not in agreement with theoretical calculations. The error does not come from these calculations, but from the fact that the Universal Time was not a uniform time scale: the Earth slowing in its rotation around its axis made the length of the average day increasing (only a few milliseconds per century , but accumulating) and therefore the duration of the second was also increasing. Such a non-uniform time scale could be used for dating events but not for measuring durations with a good accuracy. Worse, this time scale was used to determine the motions of celestial bodies in the solar system, these calculations requiring a uniform time scale .
Astronomers then introduced a new time scale , more stable, based on the revolution of the Earth around the Sun, called Ephemeris Time (ET) . The duration of the year however is not really stable either. Then, we chose to use a time scale built differently: atomic clocks measuring the frequencies of the atoms and providing a " second " particularly stable. We will then accumulate the seconds one after the other to make a time scale, the International Atomic Time (TAI) independent of celestial motions. The International Atomic Time is in fact an average of atomic clocks distributed throughout the world. Things are complicated by the fact that relativistic effects show that the second depends on the frame where we place ourselves: we arrive there at a very high level of accuracy and the ways to use these time scales are much more complex depending on the desired high accuracy. For determining the motions of the planets , using a time scale keyed to the TAI is sufficient, the relativistic effects being taken into account only for radar or similar observations. It should be noted that the second selected as a standard basis for atomic clocks was not the best choice : it is equal to 1/86400 of the mean solar day on January 1, 1900 , calculed from observations made between 1820 and 1850, which is not very happy, this choice taking effect in 1962, while the second had increased. The use of International Atomic Time , very stable, will lead to a mismatch with the rotation of the Earth and it will fail to this time scale to keep twelve o'clock at noon ... That is why was announced from time to time a second to be added on December 31 or June 30 to the time scale, depending on the variations of the rotation of the Earth. So that the usual time scale does not deviate by more than one second of the time from the astronomical Universal Time . This atomic time scale modified by the regular addition of a second is called Coordinated Universal Time (UTC). The stable and uniform time scale used for astronomical calculations is now the Terrestrial Time (TT), time scale whose practical realization is linked to International Atomic Time extending the time ephemeris from 1 January 1977.
More specifically, the time scales are interrelated as follows . The International Atomic Time (TAI) is the scale of the most uniform possible time: it is made and not based on any astronomical phenomenon. This is a time scale based on physics.
The Universal Time scale is a nonuniformly time following the rotation of the Earth; it is noted UT1 and is a linear function of the angle of rotation of the Earth. It is not predictable insofar as slowing the rotation of the Earth not regularly (see figure). It is determined a posteriori using observations. The Coordinated Universal Time (UTC) is a time linked to TAI, uniform "by intervals" , i.e. it has the metrological qualities of TAI but follows UT1 without deviating by more than one second. It is therefore readjusted if necessary by a second (see figure).
We have the relation: TAI - UTC = an integer number of seconds.
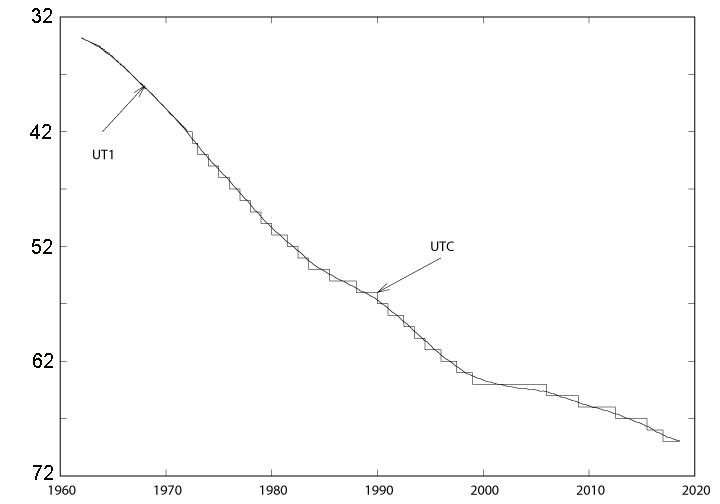
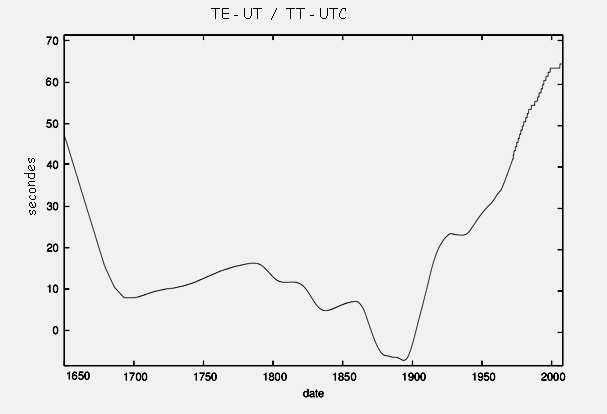
The ephemeris time (TE) is more uniform and was created to extend the Universal Time as soon as we became aware of its non-uniformity. From January 1, 1977, the TE is extended by the Terrestrial Time (TT), defined by the relationship with TAI: TT = TAI + 32.184 s. This shift of 32.184 s comes from the fact that TAI - UT1 was taken at zero at the date of January 1, 1958
since TT is derived from TE identifyed to UT1 near the year 1900 (see the figure below).
It is the relationship TE-UT or TT-UTC which is important to know since the observations are referred to UTC in all observatories and the dynamical models are made in a uniform time scale, TT. The following table shows the correspondence between TT and UTC as the difference TT-UTC (which were: TE - UT1 before 1977). The addition of a second is made either on December 31 or on June 30 at 23h 59m 60s, generally denoted wrongly January 1 or July 1.
| Interval of use | TT - UTC |
|---|---|
| 1 January 1972 - 1 July 1972 | 42.184s |
| 1 July 1972 - 1 January 1973 | 43.184s |
| 1 January 1973 - 1 January 1974 | 44.184s |
| 1 January 1974 - 1 January 1975 | 45.184s |
| 1 January 1975 - 1 January 1976 | 46.184s |
| 1 January 1976 - 1 January 1977 | 47.184s |
| 1 January 1977 - 1 January 1978 | 48.184s |
| 1 January 1978 - 1 January 1979 | 49.184s |
| 1 January 1979 - 1 January 1980 | 50.184s |
| 1 January 1980 - 1 July 1981 | 51.184s |
| 1 July 1981 - 1 July 1982 | 52.184s |
| 1 July 1982 - 1 July 1983 | 53.184s |
| 1 July 1983 - 1 July 1985 | 54.184s |
| 1 July 1985 - 1 July 1988 | 55.184s |
| 1 July 1988 - 1 January 1990 | 56.184s |
| 1 January 1990 - 1 January 1991 | 57.184s |
| 1 January 1991 - 1 July 1992 | 58.184s |
| 1 July 1992 - 1 July 1993 | 59.184s |
| 1 July 1993 - 1 July 1994 | 60.184s |
| 1 July 1994 - 1 January 1996 | 61.184s |
| 1 January 1996 - 1 July 1997 | 62.184s |
| 1 July 1997 - 1 January 1999 | 63.184s |
| 1 January 1999 - 1 January 2006 | 64.184s |
| 1 January 2006 - 1 January 2009 | 65.184s |
| 1 January 2009 - 1 July 2012 | 66,184s |
| 1 July 2012 - 1 July 2015 - | 67,184s |
| 1 July 2015 - 1 January 2017 | 68,184s |
| 1 January 2017 - | 69,184s |
The following figure gives an extrapolation in the past because this difference already slowed the Earth, even if we did not know. This extrapolation is determined from various observations such as solar eclipses and is necessary for the analysis of old observations and avoid to assign an acceleration to some bodies of the solar system, acceleration which is only the signature of the slowdown of the rotation of the Earth. Old eclipses of the Sun showed that the TT -UT value reached 3 hours two thousand years ago (see the page on eclipses).
The following figure provides the duration of day as a function of time : the decreasing speed of the rotation of the Earth around its axis has the effect of increasing the duration of the day. However, this increase (small, about 2 milliseconds by century) has a significant cumulative effect as noted above. It may be noted that this slowdown is very irregular. To the secular slowdown, we have to add variations due to the coupling between the core and the mantle of the Earth so-called "decadal variations".
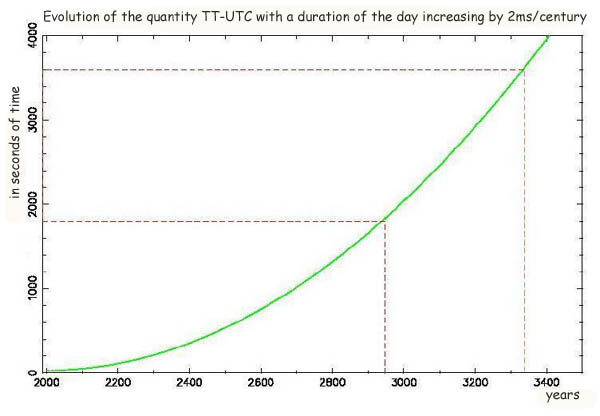
International discussion is currently underway to decide whether to stop the system of leap seconds. Thus, the time associated with the rotation of the Earth would separate from the uniform time built with atomic clocks . The figure below shows the growth of the gap TT- UTC in the future. This gap would be one that would separate us gradually from solar time if we renounced the leap seconds . In this case, we should have to add a "leap hour" around the year 3330.
Finally, let us say that the sidereal time is not a time scale : this is only an angle (the hour angle of the vernal equinox), which gives the position of the Earth around its axis. It is used to find a star in the local sky from its spherical coordinates, right ascension and declination (see paragraph devoted to it and its definition).
Definitions of different time scales can be found in the glossary..
Precession and nutation
The slowing of the Earth rotation showed us the irregularity of the rotation. In addition, the axis of rotation does not remain fixed over time: the gravitational perturbations of the Moon, the Sun and planets cause different motions that axis. First a fast oscillating "periodic" small amplitude around an average position is the nutation. Then, by a slow movement, "secular" while remaining tilted approximately 23° 26' to the ecliptic (the orbital plane of the Earth), the axis will make a complete rotation in 25 700 years. This is the precession. In a little less than 13 000 years , the polar star will be changed. It will beo the star Vega that will point the axis of rotation of the Earth and 13,000 years later it will be directed to our polar star again.
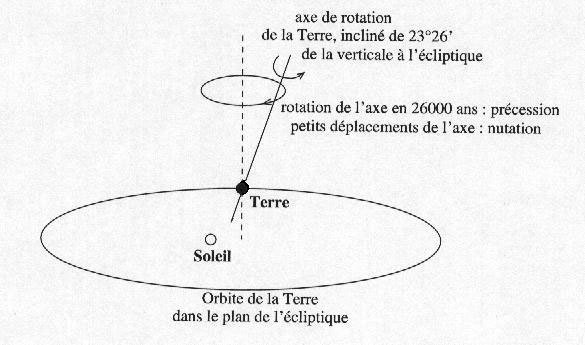
This precession motion, of course, implies that the equinox or the vernal point will rotate on our celestial sphere in 25 700 years , that is to say that the origin of right ascensions that we have chosen on our celestial sphere is mobile! This makes harder to measure the motions of stars on our celestial sphere ... The problem is solved by choosing an equinox at a given date. Thus, today, the vernal point is the origin of the beginning of the year 2000; all star catalogs use this reference. It should be noted that the observations may, in some cases, be made referred to the vernal point of the day but a correction will be made to reduce the observation to the common reference of 2000 .
Positions in a reference frame of the date are called true coordinates of the date and that in a reference frame 2000 are called "mean J2000". In the first case , we use an axis affected by nutation and precession and in the second case the nutation is removed and we take the "mean" axis of the beginning of the year 2000.
Definition of the year
The year seems to be easy to define : it is the time it takes to the Earth to make one complete revolution around the Sun. In fact it is not so simple. The year is linked to our calendar and the fact that the Earth has completed one full revolution (360°) around the Sun is not an essential criterion.
If we take a fixed direction in space, the Earth will take 365 days 6 hours 9 minutes 10 seconds to go back to the same direction. We call this duration the sidereal year.
If the direction of the vernal equinox of the date (spring equinox) is considered, the Earth will take 5h 48m 45s 365 days to go back to the direction of that point. This is a different duration than the sidereal year because the vernal point moved while the Earth revolves ... We call this duration the tropical year.
If we consider the point in the orbit of the Earth closest to the Sun (perihelion, currently on Jan. 3), the Earth will take 365 days 6h 13m 53s to go back to this point. We call this duration the anomalistic year.
If the direction of the node of the lunar orbit is considered, the Earth will take 346 days 14h 24m to go back to this point which moves rapidly, shortening the year. We call this duration the draconitic year.
It is seen that there is a choice to make to define a year. This choice will be social, cultural and religious. Our calendar (Gregorian) adopted the tropical year because it brings back seasons on the same date each year (solar calendar) . The Chinese calendar uses the sidereal year because it will follow to the motion of the stars in the zodiac (relative to the fixed stars) . The draconitic year serves only to determine the frequency of solar eclipses. Lunar calendars (such as the Muslim calendar) helps for a good approximation of the lunar month. They are independent of the motion of the Earth around the Sun.
Credit : J.E. Arlot, J.L. Simon / IMCCE



