


 Français
Français
Undersatnding > Fundamental concepts > Measures II
THE MEASURE OF DISTANCES
Measuring the Earth
Measuring the distance Earth-Moon and the size of the Moon
Measuring the distance Earth-Sun and Earth-planets
Measuring the distance to the stars
Annual parallax
Brightness of the stars
Expansion of the universe
All measurements made on the sky are measure of angles. On the celestial sphere, all the stars seem be at the same distance from Earth. The Earth itself appears flat and motionless. How to determine the shape of the Earth, how to measure its size and how to measure the distance from Earth to planets, stars ...? For this, we will make a little history, as astronomy progresses step by step, by successive approximations.
Measuring the Earth
How to measure the Earth and see that it is round? Its roundness is easily understandable and two facts had led astronomers in antiquity to admit this roundness. First, during the eclipses of the Moon, the shadow of the Earth is round. But this finding could also mean that the Earth was flat with a disk shape. It is the progressive disappearance of vessels below the horizon which suggests that the Earth is round. Now, how to measure the radius of the Earth?
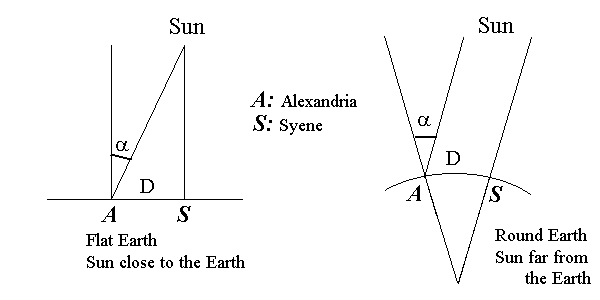
The first measure was that of Eratosthenes (c. 285-194 BC) in ancient Greece. He found that the Sun's rays were parallel, at least as Sun was very far or to infinity. He had found that the day of the solstice, at noon, the objects had no shadow at Syene (now Aswan) and could observe the Sun from the bottom of a well. This phenomenon was not observed in Alexandria 800 km further North. Eratosthenes measured the shadow of a stick in Alexandria the day of the solstice. He also had to measure the distance Alexandria-Syene (5000 stades), which was not easy at that time. This was not interpreted as a calculation of triangulation proving that the Sun was close because it was move in the North-South direction to see a change direction of the Sun. A measurement at the same local solar time (the only one available at the time) for sites located on an East-West line would have given nothing (hence the assumption that the Sun's rays were parallel). Eratosthenes was wrong only by one hundredth for the size of the Earth. Two hundred years before him, Anaxagoras made the same measurement assuming the Earth was flat, that is to say its infinite radius: it was naturally arrived at the result that the Sun was approximately 6500 km from the Earth
Measure of the distance Earth-Moon and of the size of the Moon
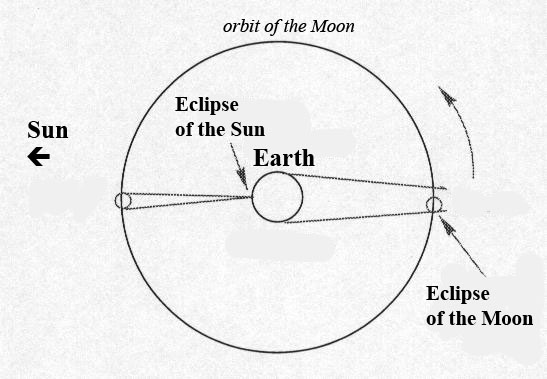
The first measurement of the size of the Moon and the distance Earth-Moon was made in antiquity by observing the eclipses. The eclipses of the Moon shows the width of the shadow of the Earth on the Moon and we see that the radius of the shadow of the Earth is 2.5 lunar diameters at the Moon. However, during a solar eclipse, the surface is on top of the cone of Earth's shadow as the area of the Earth in the shadow is small (the apparent diameters of the Moon and Sun are almost identical). The shadow of the Moon is narrowed from a lunar diameter after the Earth-Moon distance. It must be the same for the shadow of the Earth on the Moon. Therefore Earth is 2.5 +1 = 3.5 lunar diameters. Knowing the diameter of the Earth we deduce the lunar diameter in kilometers. The angle at which one sees the Moon having a half degree (1/110 radian), the Earth-Moon distance is 110 diameters of the Moon i.e. 60 Earth radii or 384,000 km away.
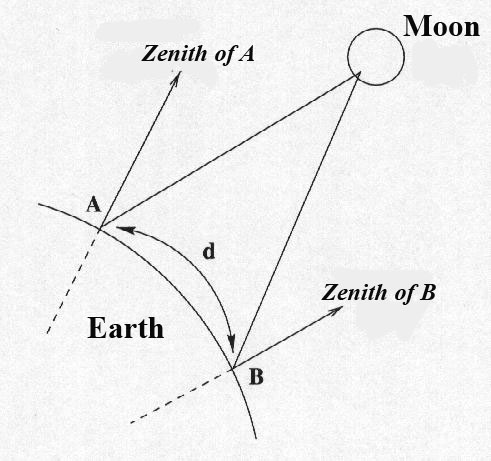
When they will have more accurate telescopes, astronomers will be able to use the triangulation method for calculating the distance Earth-Moon through observations from two distant points on Earth.
Nowadays, the distance Earth-Moon is measured using laser on a reflector put at the nsurface of the Moon by the crew of Apollo mission. The accuracy of the measurement is now a few centimeters.

Measuring the distance Earth-Sun and Earth-planets
The previous method of triangulation may well be applied to some other bodies of the solar system. But for the Sun is very difficult: it is not easy to observe, and it is much farther than the Moon. We will see that for the Sun and distant objects of the solar system, we need a theoretical model to measure and derive distances not directly accessible to measurement. Laws of Kepler and celestial mechanics will be needed to determine distances in the solar system.
Measure of the distances to the stars
The annual parallax
The distances to be measured become very large and the distance between two points on Earth is not sufficient to make triangulation. We will use the annual parallax, that is to say the different positions of the Earth in its orbit.
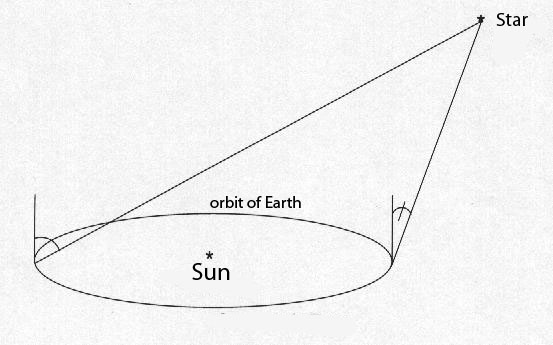
This method of measurement uses the triangulation method but waiting 6 months in ordre to have the Earth at 300 millions kilometers from its first positione.
The brightness of the stars
Another method to measure the distance to stars is to measure their brightness. Indeed, for two stars with the same brightness, the farthest will appear fainter. The apparent brightness varies as the square of the distance: a star is twice as far and four times fainter. But for deriving the distance of a star from its apparent brightness, we must know the distance of a reference star. We therefore classified the stars by their spectral type, their variability so that two similar stars emit the same amount light. If a star of a certain type is sufficiently close to the Earth so that the distance can be measured with its annual parallax, then measuring the apparent brightness of stars of the same type will provide their distance from Earth.
Expansion of the universe
The expansion of the universe gives us the means to measure distances of very distant objects. Indeed, the principle of expansion of the universe says that galaxies are moving away from each other. This movement is even more important that the object is away from Earth. Spectral analysis of the objects will determine a redshift for objects moving away us, proportional to their velocity and therefore proportional to their distance from Earth. Again, it will calibrate the distance of some objects to find distances of other objects.
We see, through these techniques which give very roughly some methods for the determination of distances of distant objects that from angle measurements on the celestial sphere, we can deduce the distance of the Moon (close) to very distant galaxies.
Credit : J.E. Arlot/IMCCE, observatoire de Paris



