


 Français
Français
Understanding > Fundamental concepts > Measures I
THE CELESTIAL SPHERE
How to find references in positional astronomy ?
DEFINING A FRAME IN THE SKY
The celestial sphere
The equatorial frame
The local frame
Determining the position of an unknown object
The meridian transit circle
The link to reference stars
Instruments
Defining a frame in the sky
When looking at the sky from the Earth's surface, how to find the bodies of the solar system, the stars, how to know where we are in space? We see a sky studded with brilliant points with some moving, but we do not have the feeling we move ourselves in space. The idea an Earth fixed at the center of the universe is a natural choice, but if looking more precisely ti the celestial bodies, things appear to be not so simple as that. Let's see how understand how it works from observations.
Tout d'abord nous devons constater que les étoiles et les planètes ne restent pas fixes sur la voûte céleste. Leurs mouvements proviennent soit du mouvement de la Terre autour de son axe (mouvement diurne), soit du mouvement de la Terre autour du Soleil (mouvement apparent des corps du Soleil et des planètes), soit du mouvement propre de ces astres (insignifiant pour les étoiles mais régulier et très détectable pour les planètes). L'astronomie de position va nous aider à déméler tous ces mouvements qui se superposent. First we must note that the stars and planets do not remain fixed in the sky. Their motions come either from the motion of the Earth around its axis (diurnal motion), or the motion of the Earth around the Sun (apparent motion of the Sun and planets), or from the proper motion of these bodies (insignificant for the stars but steady and very detectable for planets). The positional astronomy will help us to separate all these superimposed motions.
The celestial sphere
First, our perception of the sky is that of half of a sphere: all stars and planets are-apparently-to the same distance from us. Our depth perception, indeed, stops a few tens of meters from us, beyond we do not perceive relief, so no more distances but only angles.
We are, each of us, the center of a sphere on which we see the celestial bodies. This sphere is called the celestial sphere and we will measure angles on this sphere.
How to find a reference frame on this sphere ? The problem is harder when seing that the stars are moving on this sphere...
Ther solution is to proceed as we did on the surface of the Earth: drawing meridians and parallels and chosing a meridian as origin and an equator. For that, several possibilities exist.
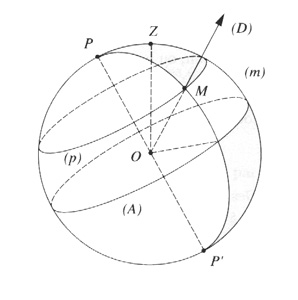
The equatorial reference frame
To determine an equator in the sky, it's pretty simple: first, notice that all the stars appear running on small circles around the polar star(it is the diurnal rotation of the Earth). Thus, the terrestrial equator projected onto the celestial sphere and draws easily a celestial equator. We have now angles on this sphere as latitudes on Earth. We call this angle a "declination" that there are -90 ° to 90 ° from the South pole to the North Pole. The North Pole is materialized by a star that seems fixed: the polar star "Polaris'.
To determine a meridian as origin, it is a little more complicated. First, the celestial sphere appears turning, which does not facilitate the choice of a prime meridian. But one can imagine it stopping. The idea the most simple would be to take any star and consider that the meridian passing through this star is the meridian origin. Besides the fact that it is not sure that the star is really fixed, such a mark is not a priori logic because this meridian would have no astronomical sense, or dynamical, because, remember that, everything moves and it is important to connect the celestial sphere to these movements. It is the rotation of the Earth around its axis which shows us the equator and the pole (motion related to the day). This will be the revolution of the Earth around the Sun, which will designate to us the meridian origin which is connected, as we shall see later, to the year.
On the celestial sphere that we stopped, the stars are fixed, but some stars (formerly called "wandering stars") move among the fixed stars: the planets, the Moon and especially the Sun, even if it hides the stars around it. The Sun follows a great circle on the sphere for one year: this is an apparent motion due to the annual revolution of the Earth around the Sun. We will say sometimes "orbit of the Sun", because from the kinematic point of view, that is to say when we do not consider the forces (dynamics), we consider that it is the Sun that runs around the Earth!
As the Earth does not revolve around the Sun in the plane of the equator (the axis of the Raeth is inclined on its orbital plane), the great circle described by the Sun on the celestial sphere intersects the celestial equator at two opposite points. Seen from Earth, the Sun crosses twice the great circle in one year. At one of the points of intersection it passes above the equator and at the other point below. The first is called the ascending node and the second is called the descending node.
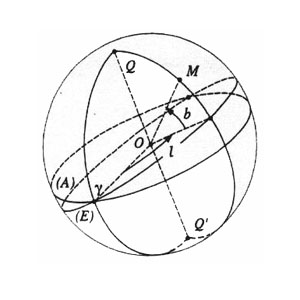
The ascending node is also called the vernal point, γ (gamma) point or spring equinox (the descending node corresponds to the autumnal equinox). Sun is at the ascending node on March 21. The great circle described by the Sun defines the orbital plane of the Earth: it is the ecliptic.
It is the meridian passing through the vernal point which will be designated as meridian origin of the celestial sphere for the equatorial frame. Longitudes of a body in such a system are called "right ascension". They are counted positively eastward from 0 to 24 hours (not 0 to 360 ° although these are angles).
One can also take the plane of the ecliptic (the plane of the revolution of the Earth around the Sun) as plane of reference. In this reference we define the pole as the pole of the ecliptic and the origin of meridian passing through the equinox (the intersection with the terrestrial equator). In this frame (ecliptic), we count the positions of the celestial bodies in longitudes and latitudes.
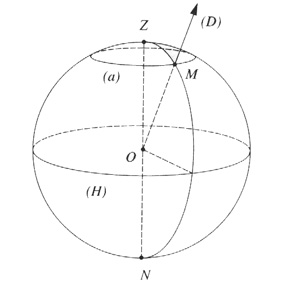
We have defined a system that allows to identify a star by its coordinates (right ascension and declination) in the sky, but one problem remains: for an observer at a given location, this marker is not fixed relative to him but moving. How to find the meridian origin to calculate a position?
The local reference frame
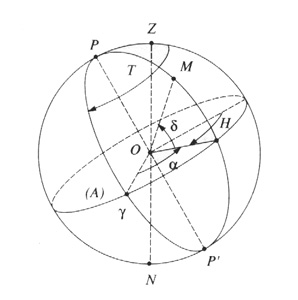
Returning back to our initial celestial sphere: we are on the surface of the Earth and we look at the sky. How to define a simple marker on the celestial sphere? The equator of reference can be defined easily by the horizontal plane around us. The latitude of a star will in fact, its altitude above the horizon. The pole will be naturally taken over our head, the zenit. The meridian origin will be taken in the direction of South because it is easy to define: that is where the stars culminate in their daily motion ( diurnal motion ). Longitude of a star in this reference frame is called azimuth.

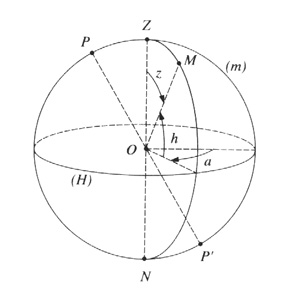
Note that the pole of the equatorial frame that we defined earlier is on the meridian origin of the local frame (called also horizontal frame). We can therefore define a local reference frame having as equator, the celestial equator and as meridian origin, the southern direction (called also local meridian). In this equatorial local reference frame, the declination of a star is the same as in the equatorial frame defined previously with equinox as origin absolute, ie independent of the rotational diurnal motion of the Earth. Contrarily, the longitude of a star will be counted from the local meridian and will be called the "hour angle" (counted in hours in the retrograde direction -towards west-). In the local coordinate frame, it should be noted that the azimuth, the altitude and hour angle vary with time for a fixed star.
Coming back to the original problem: how to find a star with known right ascension and declination? For that we need to know at any moment the position the origin of right ascensions, that is to say the vernal point (equinox). The hour angle of the vernal equinox (the angle between the vernal point and the local) is a calculable for any place : it is called "local sidereal time." It should be noted that the sidereal time is an angle, not a time even counted in hours from Oh to 24h.
So, for a given location :
Hour angle of a star H = Hour angle of the point γ - right ascension of the star α
H = T - α
knowing that the hour angle horaire of the point γ is called sidereal time T
Contrarily, finding the azimut and the altitude of a star needs to solve the spherical triangle star-North celestial pole-zenit of the place.
Finding the position of an unknown object
When observing an unknown object in the sky, how to measure its coordinates right ascension droite and declination ?
The meridian transit of a star
The oldest method is to wait until this star passes in the direction of the meridian of the place (South). At that time, its altitude is measured above the horizon (this is its maximum). Watching the local celestial spheres and the equatorial one, we understand that measuring the altitude of the star above the horizon gives the declination directly if you know the latitude of the place of observation. The problem can be reversed if the declination of the star is known, we can deduce the latitude of the place: it is the principle of the point at sea
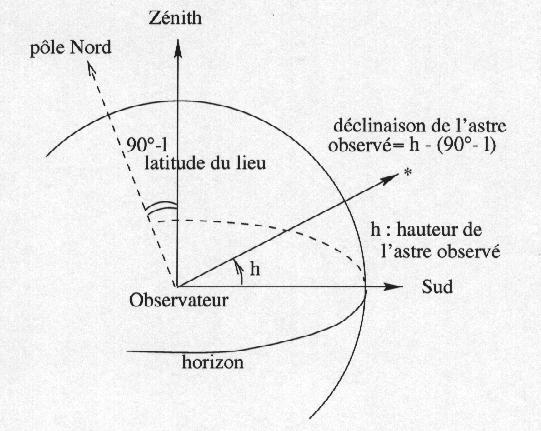
For the right ascension, it is sufficient to note the time of the meridian transit. At that time the hour angle is zero, and knowing the sidereal local time (computable), we deduce the right ascension of the star. This method has the disadvantage of making us waiting the object passing at the meridian and allow only one measurement per day. We will see observing methods allowing to make such measurements anytime.
The link to reference stars
The photographic technique or electronic imaging need
a telescope providing an image of a part of the sky, a
"field" whose size is measured in angle on the sky. In order to transform
measurements in millimeters on the image into angles on the sky requires
to have an image of the unknown object surrounded by pictures of reference stars
of which the coordinates are well known.
The process
of astrometric reduction will be used to calculate the scale of
the image that will convert millimeters into angle units
and orientation that indicates the eastern direction of the equator.
This will lead us to the positions in right ascension and
declinationt. The process of astrometric reduction is
based on these principles but is complicated for several reasons:
-picture is made so that the image plane of a piece
celestial sphere at the focus of a telescope is spherical.
we need to take this into account;
-an optical telescope is not perfect and creates distortions in the field
(no isotropy for scale or orientation) and
characteristics of the telescope (focal length of the lens) have
tendency to change with temperature;
-atmospheric refraction brings the stars towards the
zenith and a specific correction is also necessary. It
depends on the status of the atmosphere above the telescope.
These effects are taken into account by introducing more unknowns in the
reduction process. A larger number of reference stars from
catalogs is necessary to calibrate the observed field.
Star catalogs have increased significantly over recent years and we have currently dense surveys of the sky for our purpose.
Right, the field of the satellite Phoebe of Saturn, taken on March 21
1998 at 2h 52m UTC at Haute-Provence observatory
(field: 12 minutes of degree, telescope of 120 cm). The moveable body is identified as follows:
- the motion of the body is detected thanks to comparison of two successive images;
- the body is not opresent on the reference image made at another date.
A yellow arrow shows the moveable obkect, Phoebe.

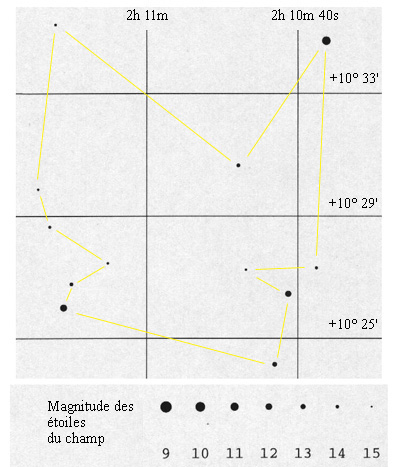
Right, the reference image without Phoebe. This image has been taken by the Schmidt telescope of the Mount Palomar observatory years before our observation of Phoebe (these images are availbale through Internet at http://www.adsabs.harvard.edu/). We have to identify the stars of the catalogue to be used for the astrometric reduction (below at right).

It remains to identify known stars of the catalog that will calibrate the field (determining the scale and orientation with respect to reference equatorial frame). At right, a field map taken from "Guide Star Catalog" a very dense star catalog constructed to allow guiding the Space Telescope..
Instruments
The instrumentation for astrometric measurements enormously
evolved over time. The old instruments allowed to measure diections with the naked eye.
It then appeared optical instruments for visual observation
using a micrometer (one had to put the star
at the cross of a reticle and read
graduated circles): it is the case of heliometers.
With photographic plates, one could keep watching after
the observation and analyze and measure quietly. First there were refractors
(type "carte du ciel") soon supplanted by Schmidt telescopes. These instruments served for systematic survey of
the sky. Photographic plates are preserved today
still useful.
Today, electronic detectors are used
CCD (charge-transfer-device) that directly provide images under numerical form
easily analyzable and measurable.

Left an instrument used by Tycho Brahe for measures of positions. This instrument has no optics: the star is seen with the naked eye, which greatly limits the number of stars observed and the the accuracy. However, measures of Tycho Brahe had the required accuracy to detect the elliptical nature of the orbits of the planets.

Left, the azimuthal quadrant used by Hevelius in 1670. Again, there is no optical mechanism but it provides a greater accuracy. Note the clocks: determining the time was fundamental to be able to model the motions in the system Solar. Today, some old observations are still used: it is however necessary they are dated in a time scale that can be connected to scales currently used nowadays.

Left, an optical instrument with a micrometer for the measure of positions and angular distances. This instrument, called heliometer, was used for very accurate measurements, especially the measure of the diameter of the Sun, hence its name. This instrument was used at the Cape observatory (South Africa) in 1896.

Left, an instrument called "carte du ciel". This refractor with 3.33 m focal length was built and installed in multiple copies in various observatories around the world (Paris, Bordeaux, Greenwich, Rio de Janeiro, ...) in order to photograph the sky for all declinations. Although not completed, this extensive work helped to improve the astrometric reference catalogs . Photographic plates made with these instruments are still used today to measure the proper motion of some stars..

Left the Schmidt telescope of the Haute-Provence observatory. As the instruments of the "carte du ciel" Schmidt telescopes were numerous. They are able to obtain photographic plates of large field (several degrees) and the whole sky was observed in this manner.

Left, the CCD detector of the 120 cm telescope of the Haute-Provence observatory, attached to Newton focus. We distinguish left the control electronics and to the right the refrigerated chamber with liquid nitrogen containing the CCD target.
Left, the astrometric satellite Hipparcos. It measured positions and proper motions of more than 100,000 stars with a precision of the order of a few milliseconds of degree. These stars are used to determine the positions of the planets in the solar system with high accuracy.

Left, the astrometric satellite Gaia. It measured positions and proper motions of more than 1,000,000,000 stars with a precision of the order of 0.001 milliseconds of degree. These stars are used to determine the positions of the planets in the solar system with high accuracy.
Credit : J.E. Arlot/IMCCE




