


 English
English
Comprendre > Concepts fondamentaux > Mesures I
LA SPHERE CELESTE
Comment se repérer en astronomie ?
COMMENT SE REPERER DANS LE CIEL ?
La sphère céleste
Le repère équatorial
Le repère local
Repérage d'un astre inconnu
Le passage d'un astre au méridien
Le rattachement aux étoiles voisines
L'instrumentation
Comment se repérer dans le ciel ?
Lorsque l'on regarde le ciel depuis le sol terrestre, comment trouver les astres du système solaire, les étoiles, comment savoir où nous nous trouvons dans l'espace ? Nous voyons une voûte céleste constellée de points brillants dont certains en mouvement, mais nous n'avons pas la sensation de nous mouvoir nous-mêmes dans l'espace. L'idée d'une Terre fixe au centre de l'univers s'impose tout naturellement, mais, à la réflexion, les choses ne sont pas si simples que cela. Voyons comment comprendre comment ça marche à partir de nos observations.
Tout d'abord nous devons constater que les étoiles et les planètes ne restent pas fixes sur la voûte céleste. Leurs mouvements proviennent soit du mouvement de la Terre autour de son axe (mouvement diurne), soit du mouvement de la Terre autour du Soleil (mouvement apparent des corps du Soleil et des planètes), soit du mouvement propre de ces astres (insignifiant pour les étoiles mais régulier et très détectable pour les planètes). L'astronomie de position va nous aider à déméler tous ces mouvements qui se superposent.
La sphère céleste
Tout d'abord, notre perception du ciel est celle d'une sphère : étoiles et planètes sont toutes -apparemment- à la même distance de nous. Notre perception du relief, en effet, s'arrête à quelques dizaines de mètres de nous : au-delà, nous ne percevons plus de relief, donc plus de distances mais seulement des angles.
Nous sommes donc, chacun d'entre nous, le centre d'une sphère sur laquelle nous voyons les corps célestes : on l'appelle la sphère céleste et on va mesurer des angles sur cette sphère.
Mais comment s'y retrouver ? D'autant plus que cette sphère semble tourner : au-dessus d'un lieu donné, on ne voit pas toujours les mêmes étoiles...
On va procéder comme sur la surface de la Terre : on va tracer des méridiens et des parallèles, choisir un méridien origine et un équateur. Pour cela il y a plusieurs façons d'aborder le problème.
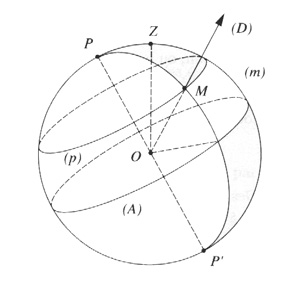
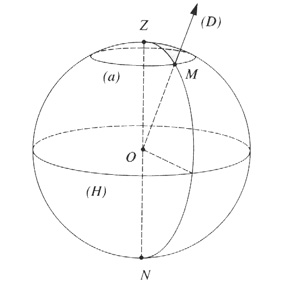
Le repère équatorial
Pour déterminer un équateur dans le ciel, c'est assez simple : on remarque tout d'abord que toutes les étoiles semblent tourner sur des petits cercles autour de l'étoile polaire (c'est le mouvement diurne de la Terre). Ainsi, l'équateur terrestre se projette sur la sphère céleste et dessine un équateur céleste aisé à trouver. Le mouvement de rotation de la Terre autour de son axe apparaît donc de cette façon. On peut maintenant compter des angles sur la sphère céleste comme les latitudes sur la Terre. On appelle cet angle une "déclinaison" que l'on compte de -90° à +90° du pôle Sud au pôle Nord. Le pôle Nord est matérialisé par une étoile qui semble fixe : l'étoile polaire.
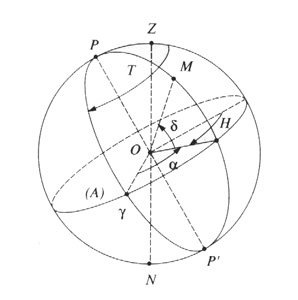
Pour déterminer un méridien origine, c'est un peu plus compliqué. Tout d'abord, la sphère céleste semble tourner, ce qui ne facilite pas le choix d'un méridien origine. Mais on peut l'imaginer s'arrêter un instant. L'idée la plus simple serait de prendre une étoile quelconque et de dire que le méridien qui passe par cet étoile est le méridien origine. Outre le fait que l'on n'est pas sûr que l'étoile est vraiment fixe, un tel repère n'est pas, a priori, logique, car un tel méridien origine n'aurait pas de sens astronomique, ni dynamique, car rappelons-le, tout bouge et il est important de relier les repères sur la sphère céleste à ces mouvements. C'est le mouvement de rotation de la Terre autour de son axe qui nous désigne l'équateur céleste (mouvement lié à la durée du jour). Ce sera le mouvement de la Terre autour du Soleil qui va nous désigner le méridien origine qui sera relié, on le verra plus tard, à l'année.
Sur la sphère céleste que nous avons arrêtée, les étoiles sont fixes mais certains astres (autrefois appelés "astres errants") s'y déplacent : les planètes, la Lune et surtout le Soleil, même si ce dernier cache les étoiles près desquelles il passe. Le Soleil décrit un grand cercle sur la sphère céleste en un an : c'est un mouvement apparent dû à la révolution annuelle de la Terre autour du Soleil. On parle ainsi souvent de l'orbite du Soleil car, au point de vue cinématique, c'est-à-dire lorsque l'on ne considère pas les forces en jeu (la dynamique), on considère que c'est le Soleil qui tourne autour de la Terre!
Comme la Terre ne tourne pas autour du Soleil dans le plan de l'équateur (l'axe de la Terre est incliné), le grand cercle décrit par le Soleil sur la sphère céleste coupe l'équateur céleste en deux points opposés. Vu de la Terre, le Soleil parcourt ce grand cercle en un an. A l'un des points d'intersection ci-dessus il passe au-dessus de l'équateur et à l'autre il passe dessous. Le premier est appelé noeud ascendant et le deuxième est appelé noeud descendant.
Le noeud ascendant est aussi appelé point vernal, point γ(gamma) ou équinoxe de printemps (le noeud descendant correspond à l'équinoxe d'automne). Le Soleil y passe au 21 mars. Le grand cercle décrit par le Soleil définit le plan orbital de la Terre : c'est l'écliptique.
C'est le méridien passant par le point vernal qui sera désigné comme méridien origine de la sphère céleste pour le repère équatorial. Les longitudes d'un astre dans un tel système sont appelées "ascensions droites". Elles sont comptées positivement vers l'est de 0 à 24 heures (et non de 0 à 360° bien que ce soient des angles).
On peut également prendre le plan de l'écliptique (le plan de la révolution de la Terre autour du Soleil) comme plan de référence. Dans ce repère on définira son pôle comme le pôle de l'écliptique et l'origine des méridiens à l'équinoxe (le point d'intersection de l'équateur terrestre). Dans ce repère (repère écliptique), on comptera les positions des astres en longitudes et latitudes.
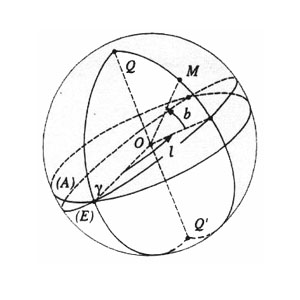
Nous avons donc défini un système qui permet de repérer un astre par ses coordonnées (ascension droite et déclinaison) dans le ciel, mais un problème subsiste : pour un observateur en un lieu donné, ce repère n'est pas fixe par rapport à lui : comment trouver le méridien origine pour calculer une position ?
Le repère local
Revenons à notre sphère céleste initiale. Nous sommes à la surface de la Terre et nous regardons le ciel. Comment définir un repère très simple sur cette sphère céleste ? L'équateur de référence peut être défini tout simplement par le plan horizontal qui nous entoure. La latitude d'un astre sera en fait sa hauteur au-dessus de l'horizon. Le pôle sera alors naturellement pris au-dessus de notre tête, au zénith. Le méridien origine sera pris dans la direction du Sud puisque c'est là que les astres culminent dans leur mouvement journalier (mouvement diurne) : il sera facile à trouver même sans aucune indication a priori. La longitude d'un astre dans ce repère sera l'azimut.

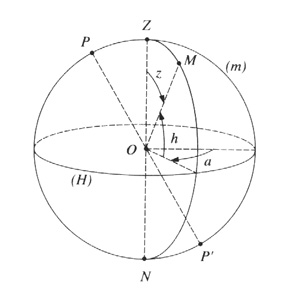
On remarque que le pôle du repère équatorial que nous avons défini précédemment se trouve sur le méridien origine du repère local (repère horizontal). On peut donc définir un repère local ayant comme équateur l'équateur céleste et comme méridien origine la direction du Sud (méridien du lieu). Dans ce repère équatorial local, la déclinaison d'une étoile est la même que dans le repère équatorial absolu, c'est à dire indépendant du mouvement de rotation diurne de la Terre. Par contre, la longitude d'un astre sera comptée à partir du méridien du lieu. On l'appellera l'"angle horaire" (compté en heures dans le sens rétrograde -vers l'ouest-). Dans le repère local, il faut noter que l'azimut, la hauteur et l'angle horaire varient au cours du temps même pour un astre fixe.
Revenons au problème initial : comment trouver une étoile dont on connaît l'ascension droite et la déclinaison ? Pour cela il nous faut connaître à chaque instant la position de l'origine des ascensions droites c'est-à-dire du point vernal (équinoxe). L'angle horaire du point vernal (l'angle séparant le point vernal du méridien du lieu) est une quantité calculable pour un lieu donné : elle est appelée "temps sidéral local". Il faut bien noter que le temps sidéral est un angle, pas un temps.
Ainsi pour un lieu donné :
Angle horaire d'une étoile H = angle horaire du point γ - ascension droite de l'étoile α
Soit H = T - α
sachant que l'angle horaire du point γ est appelé temps sidéral T
Par contre, trouver l'azimut et la hauteur d'une étoile nécessite ensuite de résoudre le triangle sphérique étoile-pôle Nord céleste-zénith du lieu.
Repérage d'un astre inconnu
Quand on observe un objet inconnu dans le ciel, comment mesure-t-on pratiquement ses coordonnées ascension droite et déclinaison ?
Le passage d'un astre au méridien
La méthode la plus ancienne consiste à attendre que cet astre passe au méridien du lieu. A ce moment, on mesure sa hauteur au-dessus de l'horizon (c'est son point culminant) et on comprend, en regardant les sphères célestes locales et équatoriales que la hauteur mesurée donne directement la déclinaison si on connaît la latitude du lieu d'observation. Le problème peut être inversé : si on connaît la déclinaison de l'astre, on peut en déduire la latitude du lieu : c'est le principe du point en mer.
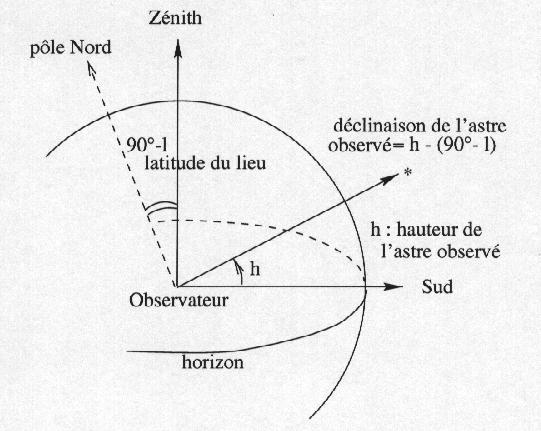
Pour l'ascension droite, il suffit de noter l'heure du passage au méridien. A ce moment l'angle horaire est nul, et connaissant le temps sidéral local (calculable), on en déduit l'ascension droite de l'astre. Cette méthode a l'inconvénient de nous faire attendre que l'astre passe au méridien et de ne permettre qu'une seule mesure par jour. Pour résoudre ce problème, on a fabriqué des instruments permettant de mesurer une hauteur pour un azimut quelconque.
Le rattachement aux étoiles voisines
La technique photographique ou d'imagerie électronique se pratique
avec un télescope fournissant une image d'une partie du ciel, un
"champ" dont la dimension est mesurée en angle sur le ciel. Transformer
des mesures en millimètres sur l'image en angles sur le ciel nécessite
d'avoir une image de l'objet inconnu entouré d'images d'étoiles
de catalogue dont on connaît les coordonnées. Le processus
de réduction astrométrique va permettre de calculer l'échelle
de l'image qui transformera des millimètres en unités d'angle
et l'orientation qui indiquera la direction de l'est selon l'équateur
céleste. Cela nous conduira aux positions en ascension droite et
déclinaison cherchées. Le processus de réduction astrométrique
repose sur ces principes mais se complique pour plusieurs raisons :
-l'image réalisée est plane alors que l'image d'un morceau
de sphère céleste au foyer d'un télescope est sphérique.
Il faut tenir compte de la projection réalisée;
-l'optique du télescope n'est pas parfaite et engendre des déformations
du champ (pas d'isotropie de l'échelle ni de l'orientation) et les
caractéristiques du télescope (focale de l'optique) ont la
fâcheuse tendance à se modifier avec la température;
-la réfraction atmosphérique rapproche les astres du
zénith : une correction spécifique est aussi nécessaire
et dépend de l'état de l'atmosphère au dessus du télescope.
Ces effets sont pris en compte en introduisant des inconnues dans le
processus de réduction. Un plus grand nombre d'étoiles de
catalogues est alors nécessaire pour étalonner le champ observé.
La haute précision astrométrique est à ce prix.
Les catalogues d'étoiles ont beaucoup progressé au cours des dernières années et on dispose actuellement d'un "bornage" ou "arpentage" dense du ciel par les étoiles de catalogue.
A droite, le champ du satellite Phoebé de Saturne, pris le 21
mars 1998 à 2h 52m UTC à l'observatoire de Haute-Provence
(champ de 12 minutes de degré, télescope de 120 cm). On identifie
l'astre mobile de deux manières :
- l'astre bouge comme cela apparaît en alternant deux poses successives;
- l'astre n'est pas présent sur une image de référence
de même champ faite avec un télescope de Schmidt à
une autre date (voir l'image ci-dessous à droite).
L'objet mobile Phoebé est indiqué par la flèche jaune.

A droite l'image de référence ne contenant pas l'astre Phoebé. Cette image a été prise avec le télescope de Schmidt de l'observatoire du Mont Palomar à une date bien antérieure. On identifie les mêmes étoiles du champ que l'on va retrouver dans le catalogue (ci-dessous à droite).

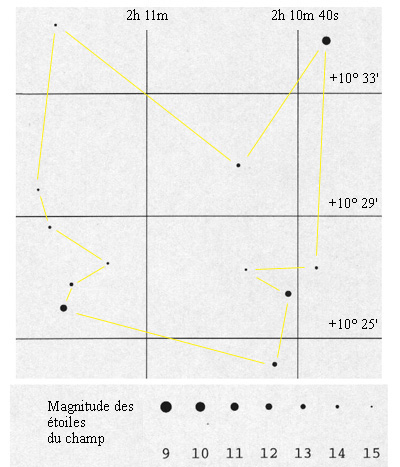
Il reste à identifier des étoiles connues de catalogue qui permettront d'étalonner le champ (détermination de l'échelle en angle par millimètre et de l'orientation par rapport au repère équatorial des ascensions droites et des déclinaisons). Ci-contre à droite une carte de champ extraite du "Guide Star catalogue", un catalogue très dense d'étoiles construit pour permettre le pointage du Télescope Spatial.
L'instrumentation
L'instrumentation pour les mesures astrométriques a énormément
évolué au cours du temps. Les instruments anciens ne faisaient
que du pointage de visée à l'oeil nu.
Sont apparus ensuite les instruments optiques à observation
visuelle à l'aide d'un micromètre (il fallait placer l'astre
à la croisée d'un réticule de visée et lire
des cercles gradués) : c'est le cas des héliomètres.
Avec la photographie, on pouvait conserver l'observation après
coup et l'analyser et la mesurer tranquillement. Il y eut d'abord les réfracteurs
(type "carte du ciel") bientôt supplantés par les télescopes
de Schmidt. Ces instruments servirent à cartographier systématiquement
le ciel. Les plaques photographiques conservées de nos jours sont
toujours utiles.
Aujourd'hui, on utilise des récepteurs électroniques
CCD (à transfert de charges) qui fournissent directement des images
numériques aisément analysables et mesurables.

Ci-contre, un instrument de mesure de positions utilisé par Tycho Brahe. Cet instrument n'est qu'un instrument de visée sans optique : l'astre est vu à l'oeil nu, ce qui limite beaucoup le nombre d'astres observables qui doivent être brillants. La précision des mesures de Tycho Brahe avait cependant la précision requise pour détecter le caractère elliptique des orbites des planètes.

Ci-contre le quadrant azimuthal utilisé par Hévélius en 1670. Là aussi, il n'y a pas d'optique mais la mécanique permet d'obtenir une plus grande précision. On remarque sur la gravure les horloges : déterminer le temps était fondamental pour pouvoir modéliser les mouvements dans le système solaire. Aujourd'hui, on utilise encore quelques observations anciennes : il est cependant nécessaire qu'elles soient datées dans une échelle de temps que l'on peut raccorder aux échelles de temps utilisées actuellement.

Ci-contre un instrument d'optique équipé d'un micromètre pour la mesure des positions et des distances. L'instrument ci-contre, appelé héliomètre, effectuait des mesures très précises et a été utilisé pour la mesure du diamètre du Soleil, d'où son nom. L'instrument présenté équipait l'observatoire du Cap (Afrique du Sud) en 1896.

Ci-contre un instrument dit "de la carte du ciel". Ce réfracteur de 3,33 m de focale fut construit en de nombreux exemplaires et installé dans divers observatoires à travers le monde (Paris, Bordeaux, Greenwich, Rio de Janeiro, ...) dans le but de photographier le ciel pour toutes les déclinaisons. Bien qu'inachevé, ce travail de grande ampleur contribua à améliorer les catalogues astrométriques de référence. les plaques photographiques réalisées sont encore exploitées aujourd'hui pour mesurer le mouvement propre de certaines étoiles.

Ci-contre le télescope de Schmidt de l'observatoire de Haute-Provence. Comme les instruments de la "carte du ciel", les télescopes de Schmidt furent fabriqués à de nombreux exemplaires. Ils permettaient d'obtenir des plaques photographiques de grand champ (plusieurs degrés) et tout le ciel a été observé de cette manière.

Ci-contre, le CCD du télescope de 120 cm de l'observatoire de Haute-Provence, fixé au foyer Newton. On distingue à gauche l'électronique de commande et à droite l'enceinte réfrigérée à l'azote liquide contenant la cible CCD.
Ci-contre le satellite astrométrique Hipparcos. Il a mesuré les positions et les mouvements propres de plus de 100 000 étoiles avec une précision de l'ordre de quelques millièmes de seconde de degré. Ces étoiles servent à la détermination des positions des astres du système solaire avec une haute précision.

Ci-contre le satellite astrométrique Gaia. Il a mesuré les positions et les mouvements propres de plus de 1 000 000 000 étoiles avec une précision de l'ordre de quelques 0,001 millièmes de seconde de degré. Ces étoiles servent à la détermination des positions des astres du système solaire avec une haute précision.
Crédit : J.E. Arlot/IMCCE




