


 English
English
Comprendre > Concepts fondamentaux > Mesures II
LA MESURE DES DISTANCES
La mesure de la Terre
Mesure de la distance Terre-Lune et de la taille de la Lune
Mesure de la distance Terre-Soleil et Terre-Planètes
Mesure des distances des étoiles
Parallaxe annuelle
Luminosité des étoiles
Expansion de l'univers
Toutes les mesures que l'on peut effectuer sur le ciel sont des mesures d'angles. Sur la sphère céleste, tous les astres semblent se trouver à la même distance de la Terre. La Terre elle-même semble plate et immobile. Comment déterminer la forme de la Terre, comment mesurer sa taille et comment mesurer la distance à la Terre des astres que nous observons ? Pour cela, nous devrons faire un peu d'histoire, car l'astronomie progresse pas à pas par "approximations successives".
La mesure de la Terre
Comment mesurer la Terre et constater qu'elle est ronde ? Sa rotondité est facilement compréhensible et deux faits avaient amené les astronomes de l'antiquité à admettre cette rotondité. D'abord, lors de l'observation des éclipses de Lune, l'ombre de la Terre est circulaire. Mais cette constatation pouvait aussi bien signifier que la Terre était plate avec une forme de disque. C'est la disparition progressive des navires sous l'horizon qui suggère bien que la Terre est ronde. Comment maintenant mesurer le rayon de la Terre ?
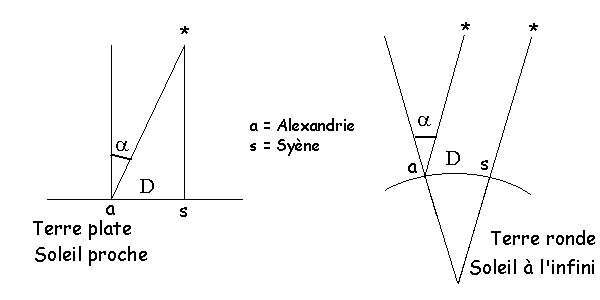
La première mesure a été celle d'Eratosthène (vers 285-194 avant J.C.) durant l'antiquité grecque. Il avait constaté que les rayons du Soleil étaient parallèles, du moins que le Soleil était très loin sinon à l'infini. Il avait constaté que le jour du solstice, à midi, les objets n'avaient pas d'ombre à Syène (aujourd'hui Assouan) et que l'on pouvait observer le Soleil du fond d'un puits. Ce phénomène n'avait pas lieu à Alexandrie 800 km plus au Nord. Eratosthène mesura donc l'ombre portée d'un bâton à Alexandrie le jour du solstice . Il lui fallait aussi mesurer la distance Alexandrie-Syène (5000 stades) ce qui n'allait pas de soi à cette époque. Cette mesure n'était pas interprêtée comme un calcul de triangulation prouvant que le Soleil était proche car il fallait se déplacer dans la direction Nord-Sud pour constater un changement de direction du Soleil. Une mesure à la même heure solaire locale (la seule disponible à l'époque) pour des lieux situés sur une ligne Est-Ouest n'aurait rien donnée (d'où la supposition que les rayons du Soleil étaient parallèles). Eratosthène ne se trompa que d'un centième sur la taille de la Terre. Deux cents ans avant lui, Anaxagore avait fait la même mesure en supposant que la Terre était plate, c'est-à-dire son rayon infini : il était naturellement arrivé au résultat que le Soleil était environ à 6500 kilomètres de la Terre.
Mesure de la distance Terre-Lune et de la taille de la Lune
La première mesure de la taille de la Lune et de la distance Terre-Lune a été réalisée dans l'antiquité au moyen de l'observation des éclipses. L'observation des éclipses de Lune montre la largeur de l'ombre de la Terre sur la Lune et on voit que le rayon de l'ombre de la terre est de 2,5 diamètres lunaires au niveau de la Lune. Or, lors d'une éclipse de Soleil, la surface terrestre est au sommet du cône d'ombre puisque la zone de la Terre dans l'ombre est petite (les diamètres apparents de la Lune et du Soleil sont quasi-identiques). L'ombre de la Lune s'est donc rétrécie d'un diamètre lunaire après la distance Terre-Lune. Il doit en être de même pour l'ombre de la Terre sur la Lune. Donc la Terre fait 2,5+1=3,5 diamètres lunaires. Connaissant le diamètre terrestre on en déduit le diamètre lunaire en kilomètres. L'angle selon lequel on voit la Lune étant d'un demi-degré (1/110 radian), la distance Terre-Lune est donc de 110 diamètres lunaires soit 60 rayons terrestres soit 384 000 km.
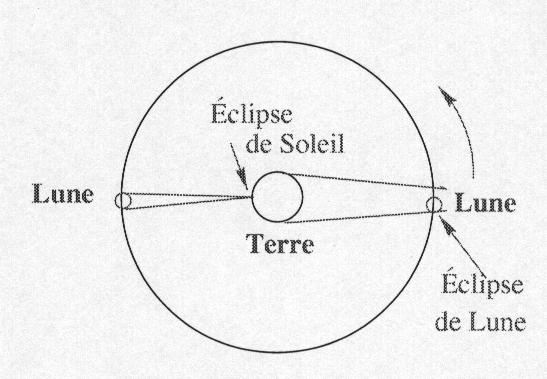
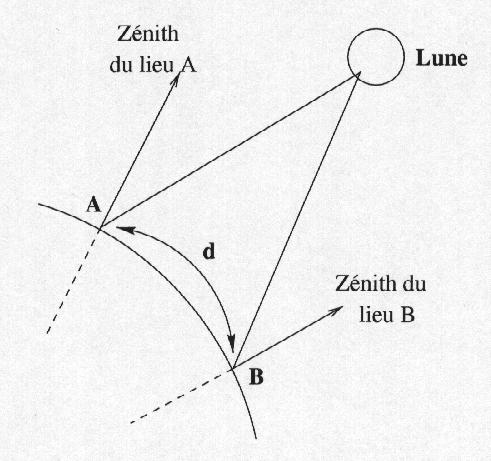
Disposant d'instruments de visée plus performants, les astronomes vont utiliser la triangulation pour mesurer la distance Terre-Lune en utilisant l'effet de parallaxe pour deux points distants à la surface de la Terre.
Aujourd'hui, on mesure la distance Terre-Lune avec des tirs laser sur un réflecteur posé à la surface de la Lune avec une précision de quelques centimètres.

Mesure de la distance Terre-Soleil et Terre-Planètes
La méthode de triangulation précédente peut bien sûr être appliquée aux autres corps du système solaire. Mais pour le Soleil, c'est très difficile : il n'est pas facile à observer et il est beaucoup plus loin que la Lune. Pour le Soleil et les objets du système solaire éloignés, nous verrons que nous aurons besoin d'un modèle théorique pour mesurer certaines distances et en déduire celles qui ne sont pas accessibles directement à la mesure. Les lois de Kepler et la mécanique céleste seront nécessaires pour la détermination des distances dans le système solaire.
Mesure des distances des étoiles
Parallaxe annuelle
Les distances à mesurer deviennent très grandes et la distance entre deux lieux sur Terre n'est pas suffisante pour faire de la triangulation. On va utiliser la parallaxe annuelle, c'est-à-dire les différentes positions de la Terre sur son orbite.
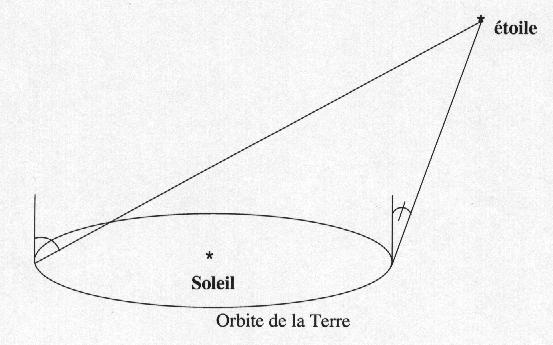
Cette mesure repose donc aussi sur la triangulation et la parallaxe mais à 6 mois d'intervalle.
Luminosité des étoiles
Une autre méthode pour mesurer la distance des étoiles est de mesurer leur luminosité. En effet, pour deux étoiles de même éclat, la plus éloignée nous paraîtra plus faible que la plus proche. La luminosité apparente varie comme le carré de la distance : une étoile deux fois plus loin est quatre fois plus faible. Mais pour déduire la distance d'une étoile de son éclat apparent, il faut connaître la distance d'une étoile de référence. On classe donc les étoiles par type : spectre, variabilité de façon à ce que deux étoiles de même type émettent la même quantité de lumière. Si une étoile d'un certain type est suffisamment proche de la Terre pour que sa distance puisse être mesurée par sa parallaxe annuelle, alors, la mesure de l'éclat apparent des étoiles de même type permettra d'en déduire leur distance à la Terre.
Expansion de l'univers
L'expansion de l'univers nous donne aussi des moyens pour mesurer les distances des objets très lointains. En effet, le principe de l'expansion de l'univers affirme que les galaxies s'éloignent les unes des autres. Ce mouvement de fuite est donc d'autant plus important que l'objet est loin de la Terre. L'analyse spectrale des objets permet de déterminer un décalage vers le rouge pour les objets qui s'éloignent de nous, proportionnel à leur vitesse et donc proportionnel à leur distance à la Terre. Encore une fois, il faudra étalonner la distance de certains objets pour connaître d'autres distances d'autres objets.
On voit, au travers de ces dernières techniques qui donnent très schématiquement des méthodes de détermination des distances des objets lointains, qu'à partir de mesures d'angles sur la sphère céleste, nous pouvons en déduire la distance de la Lune (proche) jusqu'à celles des galaxies les plus éloignées.
Crédit : J.E. Arlot/IMCCE, observatoire de Paris



