English
English
Comprendre > Concepts fondamentaux > Phénomènes II
Lever et coucher d'un astre
LEVER ET COUCHER DU SOLEIL OU D'UN AUTRE ASTRE
On a vu dans les pages sur
les saisons apparaître la notion de rotation de la Terre autour
de son axe combinée avec sa rotation autour du Soleil. La notion
de jour a été ainsi définie. On va voir dans ce chapitre,
plus précisément comment on définit et on calcule
les levers et couchers du Soleil, de la Lune et des autres astres.
Le lever et le coucher d'un astre est un phénomène astronomique
que l'on calcule à partir de ses éphémérides.
Dans le cas du Soleil, les levers et couchers définissent le jour
et la nuit et, très simplement, on dit que le Soleil se couche lorsque
sa hauteur au-dessus de l'horizon devient nulle en diminuant. De même,
on dit qu'il se lève lorsque cette hauteur devient nulle en augmentant.
Deux phénomènes viennent compliquer cette définition :
- quel est le point sur le Soleil qui est pris en compte ? En effet le Soleil présente un disque apparent d'un demi degré : le Soleil est réputé couché lorsque c'est son centre ou son bord supérieur qui a une hauteur au-dessus de l'horizon nulle.
- La réfraction atmosphérique élève les objets vers le zénith. Ainsi, la réfraction nous montre le Soleil alors que celui-ci est déjà ou encore sous l'horizon.
Pour le premier point c'est une question de définition. Les éphémérides donnent la position du centre du Soleil et si l'on veut l'heure du lever et du coucher du bord supérieur, il faudra corriger la position en conséquence, c'est-à-dire d'un demi-diamètre apparent. A noter que l'horizon est rarement visible si l'on n'est pas au bord de la mer et que cette différence importe peu.
Pour le deuxième point c'est encore une question de définition. Il va falloir prendre la réfraction en compte car c'est le lever ou le coucher du Soleil apparent qui nous importe, mais la valeur de la réfraction à l'horizon est très mal connue et on va prendre une valeur conventionnelle supposée être la moins mauvaise.
Certaines notions, que nous verrons plus loin, accompagnent les levers et couchers des astres:
- le passage au méridien (supérieur) qui est l'instant où l'astre est au plus haut dans le ciel, dans la direction du Sud. On lui associe la hauteur du Soleil à cet instant. Le passage au méridien inférieur correspond à l'instant de la nuit où le Soleil est au plus bas sous l'horizon.
- le crépuscule qui définit une période où il ne fait ni nuit, ni jour. On lui associe une hauteur négative du Soleil sous l'horizon: -6° pour le crépuscule civil, -12° pour le crépuscule nautique et -18° pour le crépuscule astronomique.
- l'azimut au lever et l'azimut au coucher qui définit la direction dans laquelle le Soleil va se lever ou se coucher.
Le calcul de l'heure du lever et du coucher
Note : tous les exemples de calcul ci-après utilisent les éphémérides publiées dans l'Annuaire du Bureau des longitudes pour 1999.
Pour calculer l'instant du lever ou du coucher d'un astre dont on suppose
connues les coordonnées équatoriales approchées α
et δ au moment du phénomène considéré,
on calcule d'abord l'angle horaire H au moment du lever ou du coucher par
la formule :
(1) cos H = (sin(h0) - sin(φ) sin(δ))/(cos(φ) cos (δ))
où φ est la latitude du lieu et h0 un angle petit qui sera
défini plus loin.
Le temps sidéral approché du lever est alors :
(2a) T = α - H
et celui du coucher,
(2b) T = α + H
On calcule ensuite, à partir de T, l'instant du phénomène
en Temps universel.
Si l'astre se déplace rapidement sur la sphère céleste
(c'est le cas pour le Soleil, certaines planètes et surtout la Lune),
on calcule pour l'instant trouvé des coordonnées α et
δ plus exactes en interpolant les tables et l'on recalcule H puis T,
par les formules (1) et (2), d'où l'instant du phénomène
en UT. Pour la Lune on est quelquefois amené à effectuer
une itération supplémentaire.
Quant à h0, son expression générale est la suivante :
h0 = P - R - 1/2 d - η1 + η2
P est la parallaxe. On la néglige pour tous les astres sauf
pour la Lune pour laquelle on la prend égale à 57'.
R est la réfraction à l'horizon. Les tables publiées
dans l'annuaire du Bureau des longitudes utilisent la théorie de
la réfraction de Radau qui conduit à R = 36' 36" mais l'on
pourra utiliser la valeur R = 34' adoptée dans les Ephémérides
Nautiques publiées par le Bureau des Longitudes et dans d'autres
publications étrangères.
1/2 d est le demi-diamètre apparent de l'astre. On l'introduit
dans la formule quand on calcule le lever et le coucher du bord supérieur
du Soleil et de la Lune et non pas le lever et le coucher du centre de
l'astre. On prend, aussi bien pour le Soleil que pour la Lune, 1/2 d =
16'.
Si l'observateur est à une altitude A au-dessus du niveau de
la mer on introduit dans h0 l'angle η1 donné par :
cos η1 = a / (a + A), où a est le rayon de la Terre.
On prend a = 6,378,140 m. On peut utiliser la formule approchée :
η1 = 1' 56" racine carrée de(A)
A étant exprimé en mètres.
Si l'on cherche le lever ou le coucher d'un astre en un lieu dont l'horizon
est limité par des collines ou des montagnes d'altitude D situées
à la distance l de l'observateur, on ajoutera à h0 l'angle
η2 tel que :
tan η2 = D/l .
On ne cherchera pas à obtenir les instants du lever ou du coucher
des astres avec une précision supérieure à une minute,
la valeur exacte de la réfraction à l'horizon au moment du
phénomène étant trop mal connue.
Exemples
1. Coucher à Bordeaux de l'étoile Sirius le 20 avril 1999
Les coordonnées moyennes de l'étoile pour 1999 sont :
α = 6h 45m 6s ; δ = - 16° 42' 53" .
En faisant les corrections de précession pour le 20 avril on
trouve :
α = 6h 45m 7s ; δ = - 16° 42' 54" .
Ici P = 0, 1/2 d = 0, η1 = 0, η2 = 0;
d'où : h0 = - R = - 34' .
Les coordonnées de Bordeaux sont :
λ = + 2m 7s ; φ = + 44° 50' 7" .
On déduit de la formule (1) :
cos H = 0,28402 ; d'où H = 73,500° = 4h 54m 0s.
Et le temps sidéral du coucher est :
T = α + H = 11h 39m 7s.
Le temps sidéral de Greenwich est donc :
T1 = T + λ = 11h 41m 14s.
Le temps sidéral de Greenwich à 0h le 20 avril 1999 est
T0 = 13h 50m 33s.
D'où :
Tt = T1 - T0 = 21h 50m 41s.
En convertissant cet intervalle de temps sidéral en un intervalle
de temps moyen on trouve que Sirius se couche à Bordeaux le 20 avril
1999 à :
t = 21h 47m 6s (UT).
2. Coucher du bord supérieur du Soleil à Paris le 26 janvier 1999
On prendra R = 34'.
On a donc :
h0 = - R - 1/2 d = - 50' .
Les coordonnées de l'observatoire de Paris sont :
λ = - 9m 21s ; φ = 48° 50' 11".
Les coordonnées du Soleil à 0h le 26 janvier sont
α = 20h 31m 44s ; δ = - 18° 52,6' .
On en déduit par la formule (1) :
H = 68,4248° = 4h 33m 42s.
D'où le temps sidéral du coucher :
T = α + H = 25h 5m 26s.
à Greenwich T1 = T + λ = 24h 56m 5s.
Le 26 janvier 1999 à 0h, le temps sidéral de Greenwich
est
T0 = 8h 19m 23s.
D'où :
Tt = T1 - T0 = 16h 36m 42s.
Ce qui, exprimé en temps moyen, donne pour heure approchée
du coucher :
t = 16h 33m 59s (UT).
Calculons, en interpolant la table de l'éphéméride
donnée par l'annuaire du Bureau des longitudes, les coordonnées
du Soleil à cet instant; on trouve :
α = 20h 34m 37s; δ = - 18° 42,2'.
En recommençant les calculs à l'aide de la formule (1)
on trouve :
H = 68,6610° = 4h 34m 39s.
D'où finalement Tt = 16h 40m 32s.
Ce qui donne pour le coucher t = 16h 37m 48s (UT).
On peut s'assurer qu'une itération supplémentaire conduirait
au même résultat que l'on considère donc comme définitif.
Or on trouve dans la table de l'éphéméride donnée
dans l'annuaire du Bureau des longitudes que le coucher du Soleil est à
16h 36m (UT). La différence est due à ce que dans la table
on donne le coucher du centre et que de plus, la réfraction à
l'horizon a été prise égale à 36' 36".
Instant approché du lever ou du coucher d'un astre
La formule suivante donne les différences des angles horaires
au lever ou au coucher d'un astre de déclinaison δ, entre un
lieu donné de latitude φ et Paris (latitude φ0) :
Δ H = +/- 5,2min x {(φ - φ0)/(1 -0,03[φ -φ0])} x tan(1,8δ
+44')
où Δ φ = φ - φ0 est exprimé en degrés
et Δ H en minutes d'heure; le signe - correspond au lever, le signe
+ au coucher.
La formule est valable, à 0,5 min près, pour δ compris
entre - 30° et + 30°. Elle permet le calcul, en Temps universel,
du lever ou du coucher du Soleil, en un lieu de latitude φ comprise entre
+ 42° et + 54°. Il suffit d'ajouter au Temps universel du lever
ou du coucher à Paris une correction égale à L + Δ
H, L étant la longitude du lieu par rapport au méridien de
Paris (comptée de 0h à 12h, positivement vers l'Ouest).
Pour la Lune (pour la France, la déclinaison de la Lune peut
être choisie égale à celle qui correspond au lever
ou au coucher à Paris) cette correction doit être multipliée
par la valeur du jour lunaire pour la date considérée, rapportée
au jour moyen. Le même mode de calcul s'applique aux planètes
et aux étoiles; la correction L + Δ H doit être multipliée
par la valeur du jour défini par l'intervalle de deux passages consécutifs
de l'astre au méridien, rapportée au jour moyen.
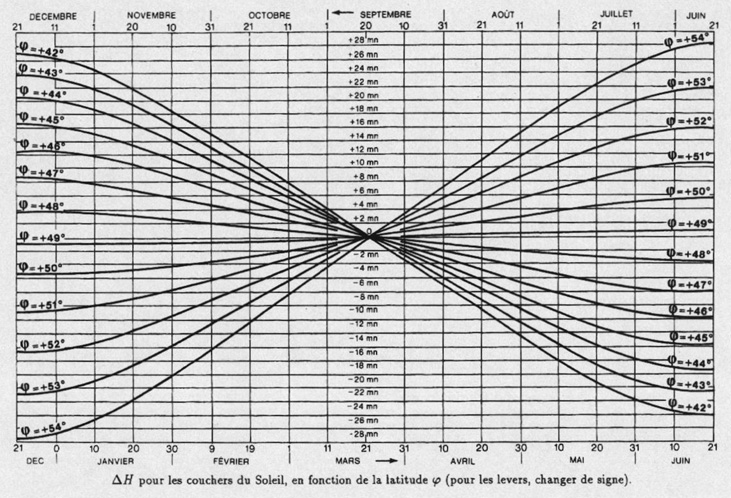
En ce qui concerne le Soleil, on trouve, ci-après, un graphique
donnant les valeurs de Δ H pour toutes les latitudes comprises entre
+ 42° et + 54°, en fonction de la date.
Azimut d'un astre à son lever et à son coucher
L'azimut a d'un astre de déclinaison
δ à son coucher en un lieu de latitude φ (α et λ
ne jouent ici aucun rôle) est donné par :
cos h0 cos a = sin(h0) tan φ - {sin(δ)/ cos(φ))
L'azimut au lever est l'opposé de l'azimut au coucher.
EXEMPLE :
Déterminons l'azimut du Soleil à Paris le 26 janvier 1999
à son coucher.
On a :
cos h0 cos a = sin(h0) tan φ - {sin(δ)/ cos(φ))
cos a = 0,4690 et a est peu différent de 62,0°
(a entre 180° et 360° pour un lever, entre 0° et 180°
pour un coucher).
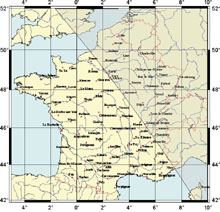
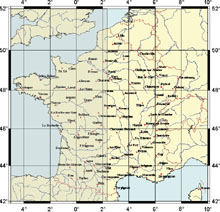
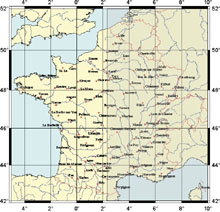
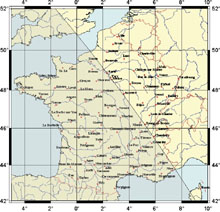
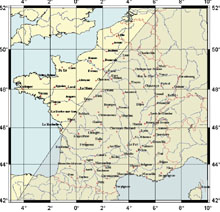
Variation de l'heure de lever et de coucher du Soleil sur le territoire français
Chacun sait que le Soleil ne se lève pas à la même heure à Paris, à Brest ou à Nice. Comment évolue cette différence ? Est-elle constante au cours de l'année ? En fait, deux facteurs interviennent, la longitude et la latitude du lieu considéré. Pour la première, on conçoit aisément que les territoires situés les plus à l'est voient le Soleil avant les autres. Pour la seconde, on sait que plus on va vers le nord en été, plus les jours sont longs, c'est-à-dire plus le Soleil se lève plus tôt et se couche plus tard. C'est le contraire en hiver. Tout cela se combine et, ainsi, le jour du solstice d'été le Soleil se lève à la même heure à Paris et à Nice mais se couche bien plus tôt à Nice qu'à Paris. Les cartes ci-dessous (cliquez dessus pour les agrandir), montrent les lieux où le Soleil se lève et se couche à la même heure qu'à Paris pour les dates des solstices et de l'équinoxe de printemps. Les zones grisées correspondent aux zones où le Soleil est couché.
ECLAIREMENT DE LA TERRE PAR LE SOLEIL
Durée du jour
On appelle jour (ne pas confondre avec le jour, unité de temps égale à 24 heures) l'intervalle de temps qui sépare le lever et
le coucher du Soleil en un lieu.
Le jour maximal a lieu au solstice d'été ou d'hiver,
suivant que la latitude est boréale ou australe; le jour minimal a lieu à l'autre solstice.
Le tableau suivant donne les durées maximale et minimale du jour à différentes latitudes.
| Latitude |
Jour maximal | Jour minimal |
|---|---|---|
| 0° | 12h 05m | 12h 05m |
| 10° | 12h 40m | 11h 30m |
| 20° | 13h 18m | 10h 53m |
| 30° | 14h 02m | 10h 10m |
| 40° | 14h 58m | 9h 16m |
| 45° | 15h 33m | 8h 42m |
| 50° | 16h 18m | 8h 0m |
| 55° | 17h 17m | 7h 5m |
| 60° | 18h 45m | 5h 45m |
| 65° | 21h 43m | 3h 22m |
| 66° | 24h 0m | 2h 30m |
| 67° 7' | 0h 0m |
A l'équateur, la durée du jour dépasse 12 h du fait de la réfraction qui nous montre le Soleil alors qu'il se trouve encore en-dessous de l'horizon.
Pour les grandes latitudes, le Soleil ne se couche pas (ou ne se lève
pas) quand la somme (ou la différence) algébrique de sa déclinaison
et de la latitude du lieu est au moins égale à 90° en
valeur absolue.
On a ainsi le jour polaire (ou la nuit polaire) dont les durées
sont données dans le tableau ci-dessous.
| Latitude boréale |
Jour polaire | Nuit polaire |
|---|---|---|
| 70° | 70 jours | 55 jours |
| 75° | 107 jours | 93 jours |
| 80° | 137 jours | 123 jours |
| 85° | 163 jours | 150 jours |
| 90° | 189 jours | 176 jours |
| Latitude australe |
Jour polaire | Nuit polaire |
|---|---|---|
| 70° | 65 jours | 59 jours |
| 75° | 101 jours | 99 jours |
| 80° | 130 jours | 130 jours |
| 85° | 156 jours | 158 jours |
| 90° | 182 jours | 183 jours |
Crépuscule
En astronomie, on appelle crépuscule la lueur, croissante avant le lever du Soleil, décroissante après son coucher, qui provient de l'éclairement des couches supérieures de l'atmosphère par les rayons de l'astre situé sous l'horizon, mais très voisin de celui-ci. Dans le langage courant, le crépuscule du matin est appelé aube ou aurore.
Le crépuscule du soir, par exemple, commence au coucher du Soleil et finit lorsque le centre du Soleil est abaissé de l'angle h au-dessous de l'horizon. On définit ainsi le crépuscule civil (h = 6°), le crépuscule nautique (h = 12°), et le crépuscule astronomique (h = 18°).
Pour connaître l'instant du début ou de la fin du crépuscule
on utilisera la formule (1) donnée dans le paragraphe concernant
les levers et couchers :
cos H = (sin(h0) - sin(φ) sin(δ))/ (cos(φ) cos (δ))
Dans cette formule h0 sera égal à - 6° pour le crépuscule
civil, - 12° pour le crépuscule nautique, et - 18° pour
le crépuscule astronomique; δ est la déclinaison du Soleil
au moment du coucher ou du lever.
On calcule ensuite, comme pour le lever ou le coucher
Tt = α +/- H + λ - T0,
où α est l'ascension droite du Soleil au lever ou au coucher,
λ la longitude du lieu, et T0 le temps sidéral de Greenwich
à 0h du jour considéré; on utilise le signe - pour
un début de crépuscule, le signe + pour une fin de crépuscule.
EXEMPLE :
Fin du crépuscule civil à Paris le 26 janvier 1999
.On a vu précédemment que le coucher du Soleil à
Paris à cette date avait lieu à 16h 37m 48s UT et que les
coordonnées du Soleil à cet instant étaient :
α = 20h 34m 37s, ; δ = - 18° 42,2'.
Par ailleurs, h0 = - 6° (crépuscule civil).
On a alors H = 77,3172° = 5h 9m 16s.
On en déduit que Tt = 17h 15m 9s et, en convertissant cet intervalle
de temps sidéral en temps moyen, que la fin du crépuscule
civil le 26 janvier 1999 a lieu à 17h 12m 19s UT.
Le crépuscule civil a donc duré :
17h 12m 19s - 16h 37m 48s = 34m 31s.
Au lieu d'effectuer le calcul ci-dessus on peut, après avoir
calculé le lever ou le coucher, calculer le début ou la fin
du crépuscule en retranchant (pour un lever) ou en ajoutant (pour
un coucher) la durée du crépuscule telle qu'on la trouve
dans les tableaux ou les graphiques ci-dessous.
Crépuscules civil, nautique et astronomique :
Crépuscule civil. --- Il commence le soir au coucher du Soleil et finit au moment où le centre de cet astre est abaissé de 6° au-dessous de l'horizon. A ce moment, si le temps est clair, commencent à paraître les planètes et les étoiles de première grandeur. Le matin, les phénomènes sont inverses.
Le Soleil ne s'abaisse pas de 6° au-dessous de l'horizon quand la
somme algébrique de sa déclinaison et de la latitude du lieu
est au moins égale à 84° en valeur absolue.
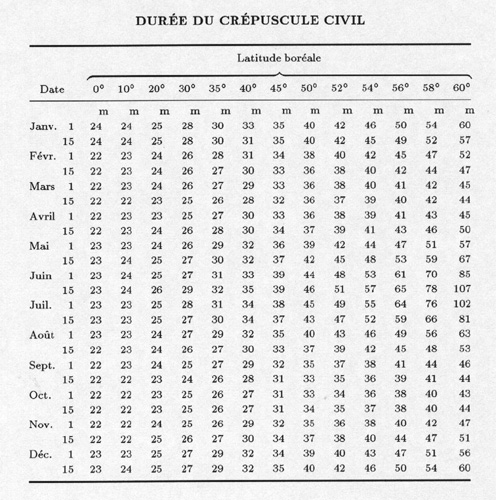
Les renseignements relatifs à la durée du crépuscule
civil en fonction de la latitude sont donnés par la table et le
graphique ci-dessous. Le premier tableau fournit, pour les latitudes
boréales de 0° à 60°, la durée, exprimée
en minutes, du crépuscule civil. Le même tableau peut être
utilisé pour les latitudes australes, à condition d'ajouter
ou de retrancher 6 mois à la date.
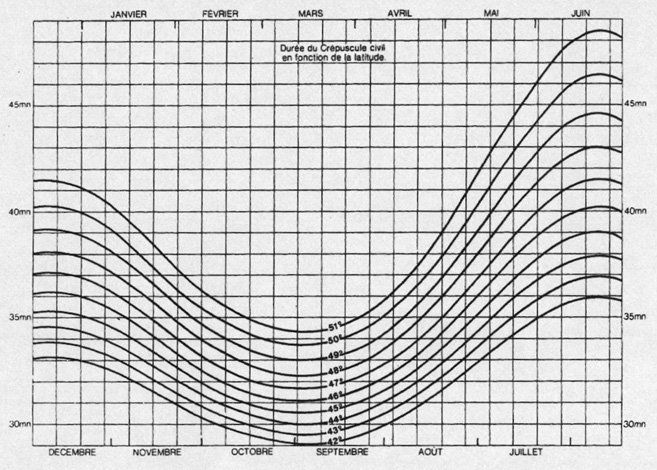
L'abaque qui suit donne directement cette durée pour les latitudes
boréales de 42° à 51°, donc en particulier pour la
France. Les traits verticaux délimitent les intervalles de temps
de 8 jours.
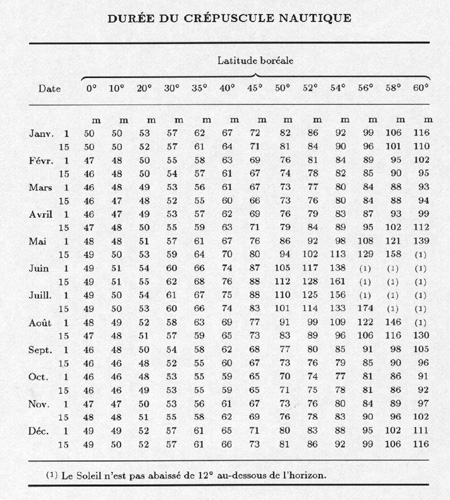
Crépuscule nautique. --- Il commence le soir au coucher
du Soleil, et finit au moment où le centre de cet astre est abaissé
de 12° au-dessous de l'horizon. A ce moment, si le temps est clair,
commencent à paraître dans le sextant les étoiles de
deuxième grandeur, alors que la ligne d'horizon est encore visible.
Le matin, les phénomènes sont inverses.
Le Soleil ne s'abaisse pas de 12° au-dessous de l'horizon quand
la somme algébrique de sa déclinaison et de la latitude du
lieu est au moins égale à 78° en valeur absolue.
Le tableau ci-après fournit, pour les latitudes boréales
de 0° à 60°, la durée, exprimée en minutes,
du crépuscule nautique. Le même tableau peut être utilisé
pour les latitudes australes, à condition d'ajouter ou de retrancher
6 mois à la date.
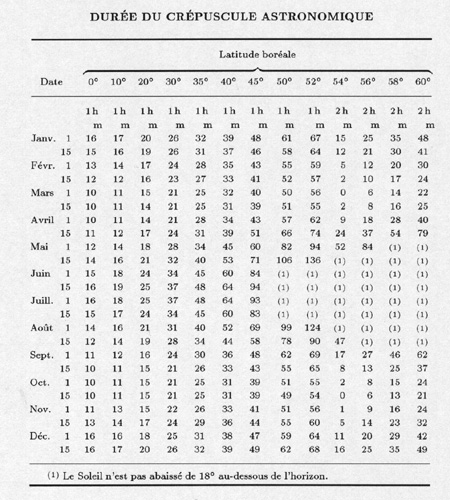
Crépuscule astronomique. --- Il commence le soir au coucher du
Soleil, et finit au moment où le centre de cet astre est abaissé
de 18° au-dessous de l'horizon. A ce moment, si le temps est clair,
apparaissent à l'oeil nu les étoiles de sixième
grandeur; il fait nuit. Le matin, les phénomènes sont
inverses.
Le Soleil ne s'abaisse pas de 18° au-dessous de l'horizon quand
la somme algébrique de sa déclinaison et de la latitude du
lieu est au moins égale à 72° en valeur absolue.
Les renseignements relatifs à la durée du crépuscule
astronomique en fonction de la latitude sont donnés dans le tableau
ci-dessous qui fournit, pour les latitudes boréales de 0° à
60°, la durée du crépuscule astronomique.
Le même tableau peut être utilisé pour les latitudes
australes, à condition d'ajouter ou de retrancher 6 mois à
la date.
Crédit : IMCCE/BDL
Cliquez ici pour obtenir les heures de levers et couchers du Soleil et de la Lune à Paris pour les années 2000, 2001, 2002 2003, 2004, 2005, 2006, 2007, 2008, 2009 et 2010.