THE ECLIPSES OF THE MOON (this section is written in French)

LES ECLIPSES DE LUNE

Quand ont lieu les éclipses de Lune ?

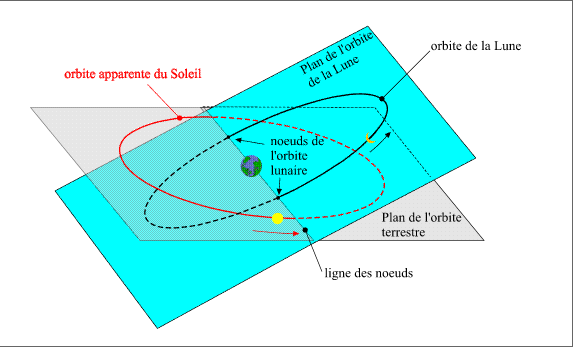
Il y a éclipse de Lune lorsque la Lune passe dans le cône d'ombre ou dans le cône de pénombre de la Terre. Le Soleil, la Terre et la Lune sont alors quasi alignés, ce qui correspond au moment de la pleine Lune. Si le plan de l'orbite de la Lune était le même que le plan de l'orbite de la Terre (écliptique), il y aurait une éclipse de Lune à chaque pleine Lune, or le plan de l'orbite de la Lune est incliné d'environ 5° 13' sur le plan de l'orbite terreste. L'intersection de ces deux plans est une droite appelée ligne des noeuds et les intersections de cette droite avec l'écliptique sont appelées noeuds de l'orbite lunaire. Pour qu'il y ait une éclipse, il faut donc que la Lune soit près de la ligne des noeuds au moment de la pleine Lune.

Périodicité des éclipses, le Saros

Lorsque la Lune et le Soleil sont au voisinage d'un des noeuds, il y a éclipse de Soleil ou éclipse de Lune. La différence entre la longitude moyenne de la Lune et celle du Soleil, est une fonction linéaire du temps qui augmente de 360° en 29.5305882 jours, cette période « L » est appelée la révolution synodique de la Lune, ou mois lunaire ou bien encore lunaison. Le plan de l'orbite de la Lune est animé d'un mouvement de précession, ainsi les noeuds parcourent l'écliptique dans le sens rétrograde (sens des aiguilles d'une montre). La période PN de ce mouvement des noeuds est de 18,61 années tropiques, soit 6797.157342 jours. La différence entre la longitude moyenne de la Lune et celle du noeud ascendant de son orbite est, comme la lunaison, une fonction linéaire du temps qui augmente de 360° en 27.2122208 jours, cette période « G » est appelée révolution draconitique de la Lune. Pour qu'il y ait retour des conditions favorables à une éclipse, on doit donc trouver une relation entre cette période et la période de la lunaison. On doit déterminer deux nombres x et y tel que x.G=y.L ou encore x/y=L/G.
En utilisant la méthode de décomposition des réels en fraction continue, on obtient entre autre :

x/y=1.085196 = 242/223

Soit une période de 223L, donc de 18ans et 11 jours. C'est ce cycle, déjà connu des Grecs, que l'on appelle le Saros. Au cours de ce cycle, on retrouve en moyenne le même nombre d'éclipses. Mais les irrégularités du mouvement de l'orbite lunaire font que la succession du type des éclipses n'est pas conservée.
En réalité, cette période n'est pas un nombre exact de jours, la fraction de jour est d'environ un tiers de jour. Donc les éclipses se reproduisent bien le même jour mais avec un décalage en longitude d'environ 120 degrés.

Nombre d'éclipses par an

On peut calculer le nombre d'éclipses observables dans une année civile. Si on tient compte de toutes les éclipses, y compris les éclipses de Lune par la pénombre, il y a au moins quatre éclipses par an, dont deux de Soleil et deux de Lune. Le nombre maximum d'éclipses par an est de sept, mais dans ce cas, il n'y aura jamais une seule éclipse de Lune (et six éclipses de Soleil) ou une seule éclipse de Soleil (et six éclipses de Lune), les autres configurations étant seules possibles.

Les canons d'éclipses

Les listes d'éclipses de Lune et de Soleil sont publiées dans des livres appelés canons d'éclipses. Le plus connu est celui de Theodor Ritter von Oppolzer, sa première édition date de 1887 dans le volume 52 des Mémoires de Mathématiques et de Sciences Naturelles de l'Académie Impériale de Vienne. Ce canon, corrigé, est réédité régulièrement par Dover Publications. Dans ce canon, on trouve 8000 éclipses de Soleil et 5200 éclipses de Lune. Il faut préciser que l'on n'y trouve pas les éclipses de Lune par la pénombre.

Il convient de citer également le canon des éclipses de Lune de Jean Meeus et Hermann Mucke (1983, Astronomisches Büro, Vienne), contenant toutes les éclipses de Lune comprises entre -2002 et +2526.

Atmosphère terrestre et éclipse de Lune

Au cours d'une éclipse totale de la Lune, les rayons lumineux passant dans l'atmosphère terrestre sont déviés par la réfraction atmosphérique et éclairent la Lune. Ce flux lumineux est plus proche au centre de la Lune et se traduit par une coloration rougeâtre, qui rappelle un peu la couleur du ciel terrestre au moment du coucher du Soleil. Les autres régions de la Lune sont peu colorées, d'une teinte généralement grise. L'aspect, les couleurs et l'intensité de l'éclairement sont très variables d'une éclipse à l'autre, ils sont imprévisibles et dépendent fortement des conditions météorologiques atmosphériques sur le terminateur terrestre (l'arc de grand cercle terrestre délimitant la surface de la Terre vue de la Lune).

Condition d'observation et durée des éclipses

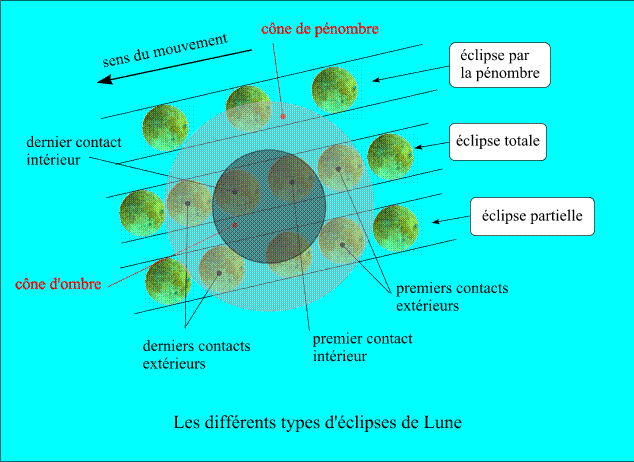
Il y a trois types d'éclipses de Lune.

Les éclipses par la pénombre, lorsque la Lune passe uniquement dans le cône de pénombre de la Terre. Ces éclipses sont très peu spectaculaires et sont à peine visibles.
Les éclipses partielles, lorsque la Lune passe en partie dans le cône d'ombre de la Terre.
Les éclipses totales, lorsque la Lune passe en totalité dans le cône d'ombre de la Terre.

Pour observer une éclipse de Lune il faut et il suffit que la Lune soit visible, donc levée au lieu d'observation.

Échelle de Temps

Les dates et les instants sont donnés en Temps universel coordonné (UTC), les longitudes des lieux sont données par rapport au méridien de Greenwich. Or l'échelle de temps utilisée dans les éphémérides est le Temps terrestre (TT), il convient donc, pour les éclipses futures de connaître une approximation de la différence entre le Temps terrestre et le Temps universel coordonné. Cette approximation est obtenue par extrapolation des valeurs actuelles. Néanmoins, lorsque l'on connaîtra la valeur exacte de cette différence, on pourra corriger les résultats publiés de la manière suivante : si dt représente la différence, en secondes de temps, entre la valeur réelle de TT-UTC et la valeur estimée de TT-UTC, alors les instants des phénomènes devront être corrigés de dt, et les longitudes de dL=1,002738.dt/240 degrés vers l'est si dt est positif ou vers l'ouest si dt est négatif.

Circonstances d'une éclipse de Lune

Chaque phase d'une éclipse est caractérisée par les instants suivants :

l'entrée dans la pénombre,
l'entrée dans l'ombre (pour les éclipses partielles et totales),
le début de la totalité (pour les éclipses totales uniquement),
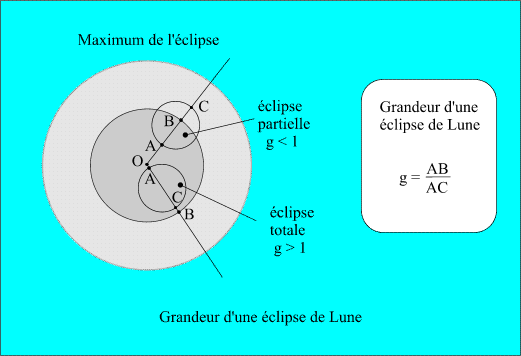
le maximum de l'éclipse et sa grandeur à cet instant,
la fin de la totalité (pour les éclipses totales uniquement),
la sortie de l'ombre (pour les éclipses partielles et totales),
la sortie de la pénombre.

Pour l'entrée et la sortie de l'ombre et de la pénombre, et pour le début et la fin de la totalité, on peut définir les points de contacts entre l'ombre ou la pénombre et le limbe lunaire. Pour l'entrée et la sortie de l'ombre et de la pénombre, on parlera de contacts extérieurs et pour le début et la fin de la totalité, de contacts intérieurs. Ces points sont donnés par leur angle polaire, défini par la direction du vecteur CO (centre de la Lune - point du contact) et la direction CP (centre de la Lune - pôle Nord), cet angle est compté positivement dans le sens rétrograde à partir du Nord.

Une éclipse de Lune pouvant durer plusieurs heures (au maximum 5 heures), pour en observer toutes les phases il faut que la Lune soit levée durant la totalité du phénomène, sinon on ne peut observer qu'une partie des phases de l'éclipse.

Pour indiquer les zones de visibilité des différentes phases, on trace ces zones sur une carte. Elles sont délimitées par les courbes qui correspondent aux terminateurs terrestres définis par les grands cercles ayant pour pôles les coordonnées des lieux où la Lune est au zénith à l'instant du début et de la fin de chaque phase. Ce sont donc les lieux du globe terrestre où la Lune est à l'horizon.

Données fournies pour chaque éclipse de Lune

On donne successivement pour chaque éclipse :

le jour ou les jours où l'éclipse se produit,
le type de l'éclipse,
le numéro de l'éclipse dans le canon d'Oppolzer (les éclipses par la pénombre ne sont pas numérotées dans ce canon),
l'instant de l'opposition avec le Soleil en ascension droite,
les coordonnées équatoriales de la Lune et du Soleil au moment de l'opposition,
les parallaxes et les demi-diamètres vrais du Soleil et de la Lune au moment de l'opposition,
les instants des débuts et fins des différentes phases de l'éclipse, ainsi que l'instant du maximum,
la grandeur de l'éclipse,
les valeurs des positions des points de contact pour chaque phase de l'éclipse, positivement dans le sens des aiguilles d'une montre à partir du Nord,
les positions géographiques des lieux qui ont la Lune au zénith pour chaque phase de l'éclipse.

Sur les cartes de visibilité, on utilise les notations suivantes :

V : la région de visibilité,
I : la région d'invisibilité,
P₁ : la limite de la région où l'on observe l'entrée dans la pénombre (pointillés larges),
O₁ : la limite de la région où l'on observe l'entrée dans l'ombre (pointillés normaux),
T₁ : la limite de la région où l'on observe l'entrée dans la totalité (petits pointillés),
T₂ : la limite de la région où l'on observe la fin de la totalité (petits pointillés),
O₂ : la limite de la région où l'on observe la sortie de l'ombre (pointillés normaux),
P₂ : la limite de la région où l'on observe la sortie de la pénombre (pointillés larges) .

accès aux prédictions d'éclipses de Lune