Réduire la taille du texte du contenu Aggrandir la taille du texte du contenu Imprimer cette page Français

Comprendre > Concepts fondamentaux

Éclipses de Soleil

Introduction



  1. Précision dans le calcul des prédictions d'éclipses
  2. Échelles de temps utilisées
  3. Recommandations
  4. Les figures
  5. Copyright


1. Précision dans le calcul des prédictions d'éclipses


Les différents organismes nationaux producteurs d'éphémérides publient dans leurs éphémérides et dans des bulletins spécifiques les circonstances générales et locales des éclipses de Lune et de Soleil.

Parmi ces organismes figurent entre autres : 

Si on compare les prédictions de ces différentes publications, on constate des écarts, sur les instants des conjonctions en longitude, sur les limites des bandes de centralité et sur les circonstances locales des éclipses. Ces écarts proviennent des différences entre les paramètres utilisés dans les calculs de prédiction.

Le premier choix porte sur les éphémérides et les théories utilisées dans le calcul des positions apparentes de la Lune et du Soleil. Tous les organismes cités ci-dessus, à l'exception du Bureau des longitudes, utilisent pour le calcul des éphémérides de la Lune et du Soleil les résultats de l'intégration numérique américaine DE200/LE200 du Jet Propulsion Laboratory. Au Bureau des longitudes nous utilisons, pour la Lune, la théorie analytique ELP2000 élaborée par M. Chapront-Touzé et J. Chapront, et pour le Soleil, la théorie analytique VSOP82 élaborée par P. Bretagnon. Ces deux théories et les éphémérides américaines sont suffisamment proches pour ne pas entraîner des écarts dans les prédictions.

Par contre tous les organismes nationaux, à l'exception de la NASA, effectuent une correction empirique en latitude et en longitude dans le calcul des éphémérides des positions apparentes de la Lune. Cette correction a pour but de passer des coordonnées du centre de masse de la Lune aux coordonnées du centre optique de la Lune. Cette correction est de +0,50" en longitude et de -0,25" en latitude. L'absence de cette correction dans les bulletins de la NASA explique les écarts constatés sur les instants de conjonction et une partie des écarts dans la détermination des lignes de centralité (décalage de la ligne de centralité).

Un deuxième paramètre important dans l'explication des écarts constatés entre les différentes prédictions, est la valeur du rayon moyen de la Lune k utilisée dans les calculs. k est exprimé en rayon terrestre. Jusqu'en 1982, on utilisait deux valeurs distinctes de k, une première (k=0,272 4880) dans le cas général et une spécifique (k=0,272 2810) uniquement pour le calcul des quantités liées à l'ombre dans le cas des éclipses totales. Le fait d'utiliser deux valeurs différentes pour les éclipses centrales posait des problèmes de discontinuité pour les éclipses mixtes. En 1982 l'Union Astronomique Internationale a recommandé d'adopter une valeur unique de k (k=0,272 5076) dans tous les calculs relatifs aux éclipses. Cette recommandation a été suivie par tous les organismes à l'exception de la NASA qui continue à utiliser deux paramètres distincts, en prenant comme première valeur de k la valeur recommandé par l'UAI (k=0,272 5076) et en étendant l'utilisation de la deuxième valeur de k (k=0, 272 2810) au cas des éclipses annulaires. Cela produit donc de nouveaux écarts entre les résultats des bulletins de la NASA et les prédictions des autres organismes, cela se traduit dans les bulletins de la NASA par une ligne de centralité plus large dans le cas des éclipses annulaires et moins large dans le cas des éclipses totales, de même cela affecte les calculs relatifs aux durées des phases centrales.

Ces choix sont la source des écarts observés entre les différentes publications et les bulletins de la NASA.

La valeur de l'aplatissement terrestre entre également dans les calculs des coordonnées géographiques des différentes lignes calculées. Mais les écarts produits par les variations possibles de cette valeur sont négligeables.

Par contre, les différences d'estimation de l'écart entre le Temps terrestre (temps uniforme) et le Temps universel (temps non uniforme lié à la rotation de la terre) affectent les résultats publiés. Cela modifie l'instant de la conjonction et les valeurs des instants et des longitudes dans les phases de l'éclipse.



2. Échelles de temps utilisées


Le temps utilisé dans les calculs des éphémérides de la Lune et du Soleil est le Temps terrestre (TT). Les longitudes des différents points de contact et les longitudes des lieux d'observations sont données par rapport au méridien de Greenwich, or pour définir des longitudes par rapport à ce méridien nous devons connaître la valeur du Temps universel (UT) le jour de l'éclipse (en toute rigueur, il s'agit du Temps universel UT1). Il faut donc connaître pour le jour de l'éclipse, la valeur de la différence TT-UT1. Cette valeur n'est pas connue à l'avance, elle est donc estimée par extrapolation à partir des valeurs disponibles au moment des prédictions. Cette valeur est indiquée dans la page donnant les circonstances de l'éclipse. Lorsque l'on connaîtra une meilleure approximation de cette différence, on pourra effectuer des corrections sur les différents instants des phénomènes et sur les longitudes des points de contact.

Nous avons volontairement donné la totalité des résultats en Temps universel et non pas en Temps universel coordonné (UTC), car on aurait alors dû faire une double estimation, celle du Temps universel pour calculer les longitudes des points de contact par rapport au méridien de Greenwich et celle du Temps universel coordonné pour afficher les résultats dans l'échelle UTC. Lorsque l'on connaîtra l'écart entre le Temps terrestre et le Temps universel coordonné, on pourra corriger les instants publiés de la manière suivante : t (en UTC)=t (en UT1)-(TT-UT1)+(TT-UTC).

Par exemple : pour l'éclipse du 11 août 1999 nous avons estimé (TT-UT1)=64,6 secondes, si la valeur de (TT-UTC) en 1999 était de 64 secondes, la correction sur les instants publiés serait alors de -0,6 seconde.

Remarque : Les calculs relatifs aux éclipses portent à la fois sur les éclipses futures et les éclipses passées. Nous utilisons pour l'édition des résultats le terme général UT pour désigner le Temps universel, en réalité ce terme représente UT1 pour les éclipses actuelles, une extrapolation de UT1 pour les éclipses futures et UT0 pour les éclipses anciennes. 



3. Recommandations


Ces écarts entre diverses publications sont source d'erreurs et de confusions, surtout aux voisinages des limites de la bande de centralité. Il convient donc d'être prudent lors de l'utilisation ou lors des calculs des données relatives aux circonstances locales au voisinage des limites de cette bande de centralité. En fonction de la publication utilisée, un lieu peut être ou ne pas être dans cette bande. Il faut savoir qu'en ces lieux, une variation de position de quelques kilomètres, peut changer de manière significative l'observation de la centralité. Pour une bonne observation de l'éclipse et pour minimiser les conséquences liées aux incertitudes sur ces calculs, il convient de se rapprocher le plus possible de la ligne de centralité. De plus pour un calcul rigoureux des instants et des positions des contacts intérieurs il est nécessaire de tenir compte de l'aspect réel du profil du limbe lunaire.



4. Les figures


Les trois corps célestes impliqués dans les calculs d'éclipses sont la Lune, la Terre et le Soleil. Le tableau suivant donne quelques caractéristiques physiques de ces corps et de leurs orbites.


Paramètres Soleil Terre Lune
Rayon  696 000 km 6 378,1363 km 1 737,4 km
Demi-grand axe de l'orbite  -------------- 149 597 870,61 km 383 398 km

 

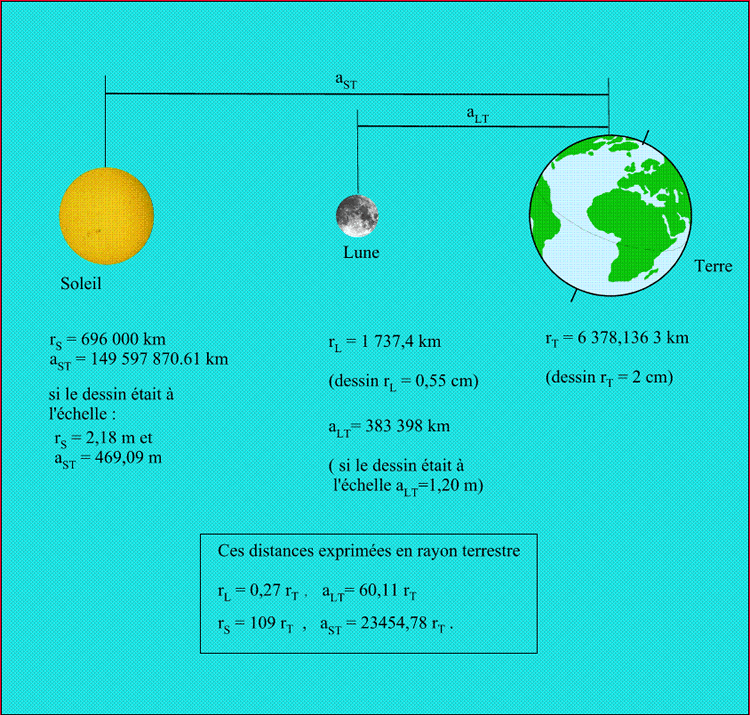
Fig 1 : Paramètres physiques : le Soleil,la Lune et la Terre

Un calcul rapide montre qu'il est impossible de produire des figures à l'échelle (voir à ce propos le chapitre sur la mesure de la distance Terre-Lune qui montre un dessin respectant les tailles des corps et distance mutuelle). Ainsi, si sur un dessin, on prenait 2 cm pour représenter le rayon terrestre, la Lune aurait un rayon de 0,55 cm et devrait être à 1,20 m de la Terre; le Soleil aurait alors un rayon de 2,18 m et serait situé à 469 m de la Terre. De même les angles qui apparaissent sur les différentes figures sont toujours très petits : 5,2° environ pour l'inclinaison de l'orbite lunaire, de l'ordre du demi-degré pour l'angle au sommet du cône d'ombre (les rayons issus du Soleil sont presque parallèles). Bien que les figures ne soient pas à l'échelle et que certains angles, pour des raisons de visibilité, aient été fortement agrandis, nous nous sommes efforcés, dans le mesure du possible, de faire des figures exactes, ainsi par exemple, la pénombre ne recouvre pas complètement la Terre, comme c'est le cas, hélas, dans certains documents.



5. Copyright


Les textes et documents (figures et cartes) fournis dans ces pages sont libres de tous droits et peuvent être reproduits dans la mesure où l'on cite l'auteur et la source des documents (P. Rocher, Institut de mécanique céleste/Observatoire de Paris/CNRS). De même les prédictions d'éclipses peuvent être reproduites, notamment les circonstances locales, en n'omettant pas de donner les paramètres utilisés pour les calculer et en indiquant la précision des calculs et les écarts possibles avec d'autres publications (voir les paragraphes précédents). Cependant dans le cadre d'une publication éditée, et conformément à la loi vous devez faire une demande d'autorisation de reproduction.


 

Crédit : P. Rocher/IMCCE