Haut de page

Glossaire

Index

Histoire de l'astronomie

Histoire des passages de Vénus devant le Soleil

English

Comprendre > Histoire > Eclipses

HISTOIRE DES ECLIPSES : 

observations et prédictions

 I. Les représentations mythologiques

Dans presque toutes les cultures anciennes et dans les sociétés sans écriture, le phénomène prodigieux qu'est une éclipse de Lune, et plus encore de Soleil, a été rapporté à une cause surnaturelle, l'intervention d'un dieu, d'un démon ou d'un génie malin menaçant d'éteindre les deux luminaires. Un événement funeste que l'on tentait ordinairement de conjurer avec force vacarme ou des formules magiques destinées à empêcher que la Lune ou le Soleil ne soient dévorés à tout jamais. En Asie, on rendait un dragon céleste responsable des éclipses (le plus ancien mot chinois pour désigner une éclipse, shih, veut dire "manger"). En Inde, c'étaient Rahu et Ketu, les deux parties du démon décapité par Vichnou correspondant respectivement aux nœuds ascendant et descendant de la Lune où se produisent les éclipses, qui cherchaient à dévorer la Lune et le Soleil. Longtemps, en Occident, les astronomes désigneront ces deux nœuds qui font un tour complet du zodiaque en 18 ans et 6 mois environ, sous l'appellation de Caput & Cauda Draconis (Tête et Queue du Dragon). En Amérique, du Canada jusqu'au Pérou en passant par le Mexique, et encore en Afrique, c'était tel animal mythique ou tel démon qui menaçait de manger soit la Lune, soit le Soleil. Quant à la Grèce ancienne, elle ne fit pas exception à la règle. D'après Démocrite (vers 460-370 av. J.-C.), les éclipses de Lune et de Soleil auraient été au nombre des événements célestes terrifiants inspirant aux hommes la croyance que des dieux en étaient les auteurs.

II. La compréhension du phénomène des éclipses

La légende de Thalès

 

Selon une légende solidement établie, Thalès de Milet (VI^e s. av. J.-C.) se serait libéré très tôt de la croyance en la causalité divine des éclipses. En effet, d'après l'historien grec Hérodote (environ 484-425 av. J.-C.), Thalès avait prédit aux Ioniens un obscurcissement du Soleil "pour l'année dans laquelle elle se produisit" (Enquête, I 74). Peu d'auteurs, tant anciens que modernes, ont mis en doute que celui qui était tenu pour un des sept Sages, ait été en état de prédire une éclipse de Soleil. D'après le Pseudo Plutarque (Opinion des philosophes, II 24), Thalès avait compris la nature du phénomène ("l'éclipse de Soleil se produit quand la Lune, dont la nature est terrestre, vient se placer à l'aplomb sous lui"). Mais cela ne lui aurait à l'évidence pas suffi pour passer au stade infiniment plus complexe de la prédiction d'une éclipse se produisant à une date précise et qui soit, en outre, visible en telle région déterminée du globe terrestre. Aux historiens qui ont fixé avec assurance la date du 28 mai 585 av. J.-C. comme étant celle de l'éclipse solaire annoncée par Thalès, l'historien américain O. Neugebauer a répondu qu'il n'existe aucun cycle pour prédire une éclipse de Soleil en un lieu donné, et que vers 600 av. J.-C. les Babyloniens, compilateurs d'éphémérides luni-solaires que Thalès aurait exploitées, n'avaient élaboré aucune théorie pour la prédiction des éclipses de Soleil. Cette légende relative à Thalès est donc au total aussi peu fiable que celle prêtant à Anaxagore (500-428 av. J.-C.) "grâce à sa connaissance de la science astronomique" (Pline l'Ancien, Histoire naturelle, II 149), la prédiction d'une chute de météorite !

 

Des Pythagoriciens à Aristote

 

Si les éclipses de Soleil sont à peu près aussi nombreuses que les éclipses de Lune quand on considère la Terre en sa totalité, on a à peu près deux fois plus de chances d'observer, en un lieu donné, une éclipse de Lune. Il reste que certaines périodes sont plus favorisées que d'autres pour observer des éclipses de Soleil dans une même région. L'historien grec Thucydide (460-vers 395 avant J.-C.) vécut dans une telle période. Il note qu'au cours de la guerre du Péloponnèse, les "éclipses de Soleil furent plus nombreuses qu'à tout autre époque historique" (La Guerre du Péloponnèse, I 23). Cette assertion est confirmée par F. Richard Stephenson (voir Bibliographie) qui date les deux éclipses solaires mentionnées par Thucydide (op. cit. II 28 et IV 52) respectivement du 3 août 431 et du 21 mars 424 av. J.-C. La première éclipse (annulaire, visible à Athènes) est décrite en ces termes par l'auteur grec, qui pourrait faire état d'une observation personnelle : " Un jour de Nouvelle Lune (c'est le seul moment semble-t-il où ce phénomène puisse se produire) il y eut en début d'après midi une éclipse de Soleil. Celui-ci prit la forme d'un croissant et quelques étoiles devinrent visibles ; puis il reprit sa forme normale ".

Au dire d'Aristote (384-322 av. J.-C.), les Pythagoriciens, qui tenaient les éclipses lunaires pour plus nombreuses dans l'absolu que les éclipses solaires, avaient essayé de rendre compte de ce fait en conjecturant que ce n'était pas seulement la Terre, mais une autre Terre, dite anti-Terre, située à l'opposé de la nôtre et que nous ne voyons pas, qui s'interposait aussi entre la Lune et sa source d'éclairement (Traité du ciel, II 13). Pour gratuite que soit cette hypothèse, elle suppose que les Pythagoriciens, et notamment Philolaos (vers 470-390 avant J.-C.), avaient compris le mécanisme général des éclipses qui postule que les corps célestes sont dotés d'une figure sphérique, que les uns sont opaques et les autres lumineux, et que c'est la position qu'ils occupent par rapport au globe terrestre, à la surface duquel l'observateur est situé, qui détermine pour un temps l'obscurcissement partiel ou total de la Lune ou du Soleil. Quant à Aristote, il est semble-t-il le premier à avoir mentionné parmi les preuves "sensibles" de la rotondité de la Terre la figure que celle-ci projette sur la Lune lorsqu'elle l'éclipse : "lors des éclipses, la Lune a toujours pour limite une ligne courbe : par conséquent, comme l'éclipse est due à l'interposition de la Terre, c'est la forme de la surface de la Terre qui est cause de la forme de cette ligne" (Traité du ciel, II 14).
Les différents types d'éclipses solaires.
 
 
Géminos (vers 50), dans son Introduction aux phénomènes, X 1-6, semble offrir le premier exposé synthétique touchant la cause et les différents types d'éclipse solaire. Il précise que le passage de la Lune sous le Soleil (c'est-à-dire lorsqu'elle est en "synode", ou conjonction, avec lui) cause une interception de la lumière solaire, si bien qu'il faudrait en toute rigueur et la remarque frappe par sa justesse parler dans ce cas d'interposition et non pas d'éclipse du Soleil : "Jamais en effet la plus petite parcelle de Soleil ne s'éclipse ; elle nous devient seulement invisible par interposition de la Lune". Par suite, ajoute Géminos, les éclipses ne sont pas identiques en tous lieux, et il y a de grands écarts dans la dimension des éclipses selon les différents climats : en un même instant, le Soleil s'éclipse ici tout à fait, c'est-à-dire pour les lieux situés à l'alignement de l'interposition, ailleurs, dans les lieux situés légèrement en dehors de la ligne d'interposition, il s'éclipse partiellement ; ailleurs encore, on ne voit pas le plus petit début d'éclipse.
La prévision : connaissance des cycles et modèles géométriques
 
Ce n'est véritablement qu'avec l'Almageste, la plus grande œuvre astronomique de l'Antiquité due à l'astronome Claude Ptolémée (II^e siècle de notre ère), que le calcul des éclipses de Soleil devient possible, mais pas encore celui de leur zone globale de visibilité. On avait reconnu depuis longtemps que les éclipses de Soleil nécessitent deux conditions : que la Lune soit nouvelle et qu'elle soit proche, comme le Soleil, de l'un de ses nœuds. Prévoir une éclipse de Soleil suppose donc que l'on dispose d'une théorie du mouvement de la Lune et d'une théorie du mouvement du Soleil. Si la théorie de ce dernier mouvement ne posait pas de problème, il n'en allait pas de même dans le cas de la Lune. Notre satellite possède un mouvement complexe en longitude, affecté de nombreuses inégalités. L'observation avait permis de découvrir dans l'antiquité les deux plus importantes, l'équation du centre (déjà connue d'Hipparque) et l'évection, justement découverte par Ptolémée. L'auteur de l'Almageste savait également que la parallaxe lunaire qui peut dépasser 1° affecte de façon non négligeable la latitude géocentrique de la Lune, c'est-à-dire sa distance angulaire à l'écliptique. Enfin, Ptolémée connaissait les diamètres apparents du Soleil et de la Lune mis en rapport avec leur distance à la Terre. C'est ce dernier point qui fait toute la supériorité de l'astronomie grecque sur l'astronomie babylonienne. Car même à son apogée, c'est-à-dire de 300 av. J.-C. jusqu'au début de notre ère, l'astronomie babylonienne n'est capable de prédire que la possibilité ou l'impossibilité d'une éclipse de Soleil. Les éphémérides babyloniennes, qui ne reposent sur aucun modèle géométrique, mais uniquement sur des fonctions arithmétiques, sont néanmoins capables de prévoir, aussi bien que Ptolémée, les coordonnées du Soleil et de la Lune. Mais l'absence de données sur les dimensions relatives de ces deux astres empêche toute prévision sur la visibilité de l'éclipse.

Le calcul d'une éclipse de Soleil se déroule dans l'Almageste en trois étapes. Dans un premier temps, Ptolémée calcule la distance angulaire de la Lune à l'un de ses nœuds. Ceux-ci ne sont d'ailleurs pas fixes : on a reconnu assez tôt qu'ils se déplaçaient sur l'écliptique, et l'observation a permis de déterminer leur période moyenne de révolution. Tous ces calculs étaient facilités par des tables, de sorte qu'il était assez aisé de prévoir d'une année sur l'autre les dates où une éclipse de Soleil était possible. On savait du reste que les éclipses se produisent sensiblement tous les six mois, lorsque le Soleil franchit un nœud de l'orbite lunaire (année draconitique).

Dans un deuxième temps, Ptolémée détermine, au voisinage de la date où l'éclipse est possible, l'instant de la conjonction Lune-Soleil, autrement dit l'instant de la Nouvelle Lune. Il dispose pour cela d'une bonne valeur du mois synodique (intervalle moyen entre deux Nouvelles Lunes) qui lui donne l'instant de la conjonction moyenne, puis, après correction de certaines inégalités, l'instant de la conjonction vraie. A ce stade du calcul, il est déjà possible de dire si l'éclipse sera ou non visible : une conjonction ayant lieu en pleine nuit par exemple est évidemment invisible.

De l'antiquité jusqu'au XVII^e siècle, les astronomes chercheront les conditions d'éclipse à l'endroit où se trouve l'observateur et non pour la Terre en général, comme on le fait aujourd'hui en astronomie moderne. Il s'agit donc de calculer, pour une certaine zone en latitude, les conditions d'existence de l'éclipse. Ce problème, l'un des plus complexes développés dans l'Almageste, est traité en utilisant les effets de la parallaxe sur les coordonnées écliptiques de la Lune. Non seulement l'Almageste permet de savoir si l'éclipse est partielle ou totale en un certain lieu (la grandeur est exprimée en doigts), mais il rend possible aussi de calculer sa durée et les instants du premier et du dernier contact.

On notera au passage qu'à aucun moment Ptolémée n'utilise la période de 223 lunaisons - improprement appelée Saros par Edmond Halley - pour prévoir une éclipse de Soleil. Une précision s'impose ici concernant cette période prétendument utilisée par les Babyloniens pour la prédiction des éclipses solaires. Halley publia en 1692 dans les Philosophical Transactions un mémoire dans lequel il proposait de corriger un passage de Pline l'Ancien (23-79 ap. J.-C.), où il était question d'une période au terme de laquelle les éclipses se reproduisent dans le même ordre. Certains manuscrits de l'Histoire naturelle circulant à l'époque contenaient des variantes, et dans celui qu'il possédait Halley a pu lire : " Il est sûr que les éclipses se reproduisent dans le même ordre au bout de 222 mois [Defectus CCXXII mensibus redire in suos orbes], et que le Soleil s'éclipse seulement lorsque la Lune achève ou commence son cours, c'est-à-dire au moment de la conjonction " (Histoire naturelle, II 56). Halley corrigea, à bon droit, 222 en 223 (CCXXIII). Mais en consultant la Souda, encyclopédie byzantine écrite au X^e siècle par un groupe d'érudits (que l'on a longtemps pris pour un savant du nom de Suidas), il trouva mention du mot dans les termes suivants : " Saros, mesure et nombre chez les Chaldéens. Un saros contient 222 mois lunaires qui font 18 ans et six mois. 120 saros correspondent à 2222 (sic pour 2220) années ". Croyant à tort que la Souda dépendait ici de Pline (qui n'emploie pas le terme Saros), Halley en conclut que les Babyloniens entendaient par là une période de 223 lunaisons ramenant les éclipses. Mais la Souda dit expressément que 222 mois = 18,5 ans, soit une année de 12 mois exactement (222/18,5 = 12). Or le calendrier babylonien est lunaire, et la durée des mois variable.

En conclusion, la période nommée Saros chez les Babyloniens n'a rien à voir avec les éclipses. L'erreur de Halley avait été dénoncée par l'astronome français Guillaume Le Gentil de la Galaisière (1725-1792) dans deux articles très critiques publiés en 1756 : mais ce dernier ne sera pas entendu et depuis, malgré le correctif apporté par nombre d'historiens des sciences, le mot Saros continue de désigner une période de 223 lunaisons, ou 18 ans 11 jours, ou encore 6585 jours, à l'issue de laquelle les éclipses de Soleil et de Lune se reproduisent dans le même ordre.

III. La détermination des zones de visibilité des éclipses de Soleil

La méthode exposée dans l'Almageste ne subira pratiquement aucune modification jusqu'au XVII^e siècle. On mentionnera néanmoins le grand astronome arabe Al-Battani (milieu IXè-929), qui conclura à la variation du diamètre apparent du Soleil, et donc à la possibilité d'éclipses de Soleil annulaires. Copernic (1473-1543), dans son De revolutionibus orbium coelestium paru en 1543, reprendra pratiquement point par point la méthode de Ptolémée, sans y apporter d'amélioration. Une étude complète a montré que cette méthode permettait de détecter pratiquement toutes les éclipses de Soleil ; seules les éclipses faibles, intéressant les régions polaires, échappaient à l'investigation des Anciens.

A partir du XVI^e siècle, on assiste à une augmentation des publications d'éphémérides en Europe ; elles prévoient toutes très correctement les éclipses de Soleil et leur visibilité. Il existe d'ailleurs, depuis le Moyen âge, des tables spéciales qui prévoient les éclipses très longtemps à l'avance. Les travaux de Tycho Brahe (1546-1601), puis de Kepler (1571-1630), ne feront qu'augmenter la précision des théories du Soleil et de la Lune ; cette quête de précision ne fera que croître après Newton et la naissance de la mécanique céleste.

Au XIX^e siècle, l'astronome allemand Friedrich Bessel (1784-1846) mettra au point une méthode, toujours utilisée, pour faciliter le calcul des circonstances locales et générales d'une éclipse de Soleil. Tous ces progrès ont surtout été possibles en raison d'une connaissance sans cesse améliorée des distances Terre-Lune et Terre-Soleil depuis le XVII^e siècle. Mais même encore au début du XX^e siècle, le tracé précis de la bande de totalité sur une carte comportait des incertitudes de quelques kilomètres dues à l'imperfection de la théorie de la Lune ; à quoi s'ajoutent, comme on le verra plus bas, les irrégularités de la rotation propre de la Terre.

 

IV. Les éclipses historiques

Nous terminerons par quelques exemples du parti que peuvent tirer de la connaissance des éclipses solaires du passé non seulement les historiens de l'astronomie, mais aussi les historiens et les astronomes.

On évoquera pour commencer la façon dont fut traité par la science astronomique du Moyen Age le cas d'une éclipse d'un genre bien particulier. Le De Sphaera de Jean de Sacrobosco (XIII^e siècle), un traité qui sera lu et commenté jusqu'au XVII^e siècle, se termine en effet sur l'interrogation suivante, née de la lecture d'un passage des Évangiles : "Quand ce fut la sixième heure, il y eut des ténèbres sur toute la terre, jusqu'à la neuvième heure " (Évangile selon Marc, 15, 33). La question posée était de savoir si l'éclipse de Soleil qui eut lieu lors de la Passion du Seigneur était naturelle ou au contraire miraculeuse. Question à quoi la théorie ptoléméenne des éclipses parfaitement assimilée par les médiévaux permit d'apporter une réponse dépourvue de toute ambiguïté : il ne pouvait pas s'agir d'un phénomène naturel puisqu'une éclipse de Soleil se produit nécessairement lorsque la Lune est nouvelle : or le Christ fut crucifié à Pâques, alors que la Lune était pleine des commentateurs de Sacrobosco ajouteront dans le même sens la durée inhabituelle de cette éclipse. Il s'est donc agi d'un miracle à travers lequel s'est manifestée la toute puissance de Dieu. Une légende (qui confond allègrement plusieurs personnages du nom de Denys) veut qu'apprenant de l'apôtre Paul la vraie nature de l'obscurcissement du ciel qu'il avait observé à Athènes, Denys l'Aréopagite se serait converti au christianisme, qu'il aurait gagné ensuite la France, dont il aurait converti les habitants ; devenu évêque de Paris, il aurait fini martyr.

La mention d'un phénomène céleste exceptionnel et / ou spectaculaire, accompagnant un événement religieux, politique ou militaire, et destinée à en souligner l'importance les comètes étaient aussi fréquemment convoquées à cette fin n'est pas rare dans les chroniques anciennes. Or, la connaissance précise des éclipses solaires qui se sont produites dans le passé permet aux historiens de vérifier, et éventuellement d'invalider, les récits de certains auteurs. C'est par exemple le cas pour l'éclipse mentionnée par l'historien byzantin Zozime (fin V^e - début VI^e siècle) dans son Histoire nouvelle (IV, 58). À propos de la bataille qui eut lieu le 5 septembre 394 dans les Alpes Juliennes entre Eugène, Arbogast et Théodose, Zozime écrit : " Lorsqu'Eugène marcha à leur rencontre avec l'ensemble de ses troupes et que les armées en vinrent aux mains l'une avec l'autre, il se produisit au moment même du combat une éclipse de Soleil si complète qu'il sembla plutôt faire nuit que jour pendant un laps de temps considérable ". L'indication par Zozime d'une éclipse qui dura un temps considérable est suspecte, et pour cause : il n'y eut pas d'éclipse de Soleil le 5 septembre 394 !

On peut aussi, à partir d'une éclipse de Soleil, dater un événement sur lequel les sources manuscrites ne fournissent que des indications chronologiques plus ou moins vagues. On a ignoré longtemps l'année exacte de la mort de l'empereur d'Occident Louis Ier le Pieux, fils de Charlemagne. On disposait seulement du témoignage consigné dans une chronique médiévale d'après lequel l'année où l'empereur Louis mourut "il y eut une éclipse de Soleil le mercredi avant l'Ascension" (eclipsis solis facta est IV. feria ante ascensionem domini). Or le calcul montre qu'une éclipse totale de Soleil fut visible en Europe le 5 mai 840, veille de l'Ascension. L'empereur est donc mort en 840.

V. Éclipses anciennes et méthodes modernes d'analyse

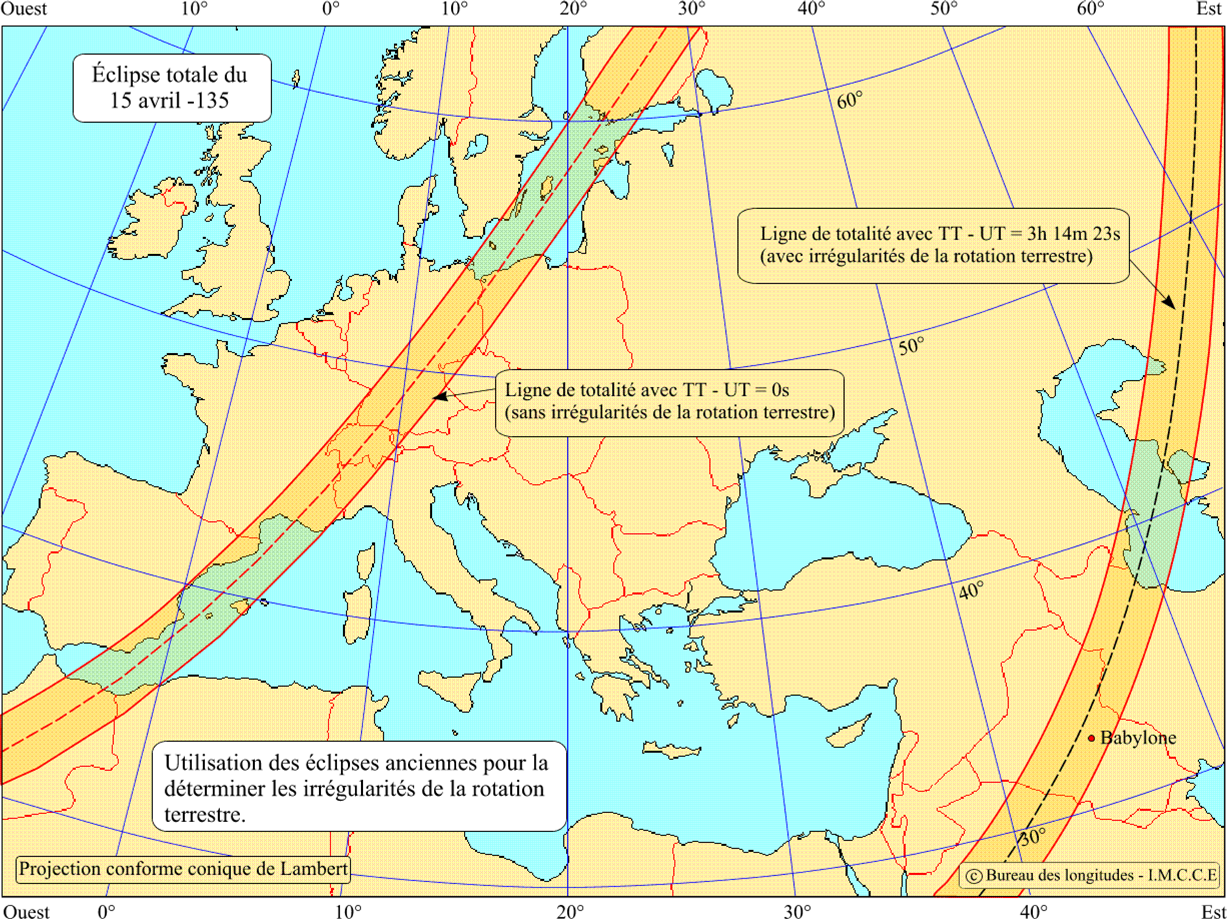
Les astronomes n'exploitent plus aujourd'hui les éclipses de Soleil en vue d'améliorer la théorie de la mécanique céleste, mais ils continuent de tirer des enseignements essentiels des éclipses anciennes. En 1749, l'astronome anglais Richard Dunthorne (1711-1775) utilisa des éclipses mentionnées par Ptolémée. En recalculant ces éclipses, Dunthorne mit en évidence un désaccord régulier entre les instants calculés et ceux observés : le mouvement de la Lune semblait s'accélérer de 20'' par siècle. Ce n'est qu'au XIX^e siècle que le problème fut résolu : ce n'est pas la Lune qui accélère, c'est la Terre qui tourne plus lentement sur son axe par suite du frottement des mers sur les fonds océaniques. Puisque la rotation de la Terre se ralentit de façon constante indépendamment d'irrégularités saisonnières , le calcul a posteriori des éclipses anciennes doit donc prendre en compte ce ralentissement, sous peine de décalages importants. On sait par exemple d'après des sources babyloniennes qu'une éclipse totale de Soleil eut lieu à Babylone le 15 avril 136 avant J.-C. Si l'on recalcule, avec les théories modernes, les circonstances de cette éclipse sans tenir compte du ralentissement de la rotation de la Terre, on trouve que la bande de totalité passait non pas à Babylone (située dans l'Irak actuel à environ 160 km au sud de Bagdad), mais au Maroc comme on le voit sur la carte ci-dessous. On voit à partir de cet exemple et de nombreux autres étudiés récemment de façon magistrale par F. Richard Stephenson que les astronomes d'aujourd'hui tirent grand profit des mentions d'éclipses anciennes pour mettre en évidence les fluctuations de la rotation de la Terre. Ainsi, la Terre ralentit de 1,6 millième de seconde par siècle (c'est-à-dire que la durée du jour augmente de 1.6 ms par siècle), ce qui, cumulé, donne un écart de l'ordre de 4 heures pour l'éclipse de babylone. Cela montre aussi les limites de la mécanique céleste actuelle : toute prévision de la zone de totalité d'une éclipse de Soleil ne peut, à l'échelle de quelques siècles, être d'une précision absolue en raison des irrégularités dans la rotation de notre planète, impossibles à déterminer à l'avance.

VI. Les dernières éclipses totales observées en France

Le 22 mai 1724, une éclipse totale visible à Paris s'est produite. Elle a eu lieu de 17h 42m à 19h 29m Temps Universel. Elle a été totale à Paris entre 18h 35m 45s et 18h 38m 13s soit pendant une durée de 2m 28s. On trouvera ci-après la carte de prédiction réalisée à l'époque.

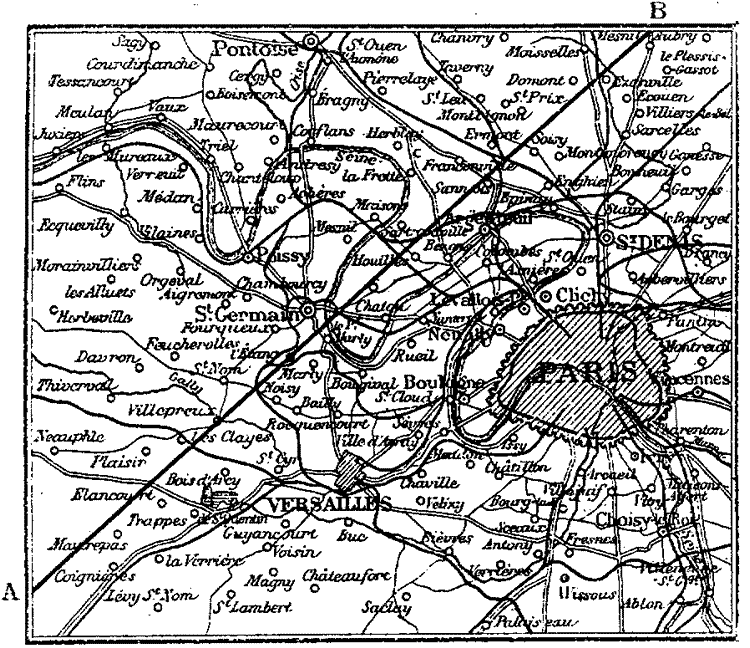
Le 17 avril 1912, une éclipse centrale annulaire pour certains lieux et totale pour d'autres du fait de la variation de la distance Terre-Lune a été observée dans la région parisienne. La totalité était visible seulement sur une ligne passant à l'ouest de Paris vers 12h 20m (temps civil de Paris). Cependant, sur la partie belge de la ligne et plus au nord, l'éclipse était visible comme annulaire. En dehors de cette ligne, l'éclipse était vue comme partielle. Ci-dessous, la carte montrant la ligne A-B d'observation.

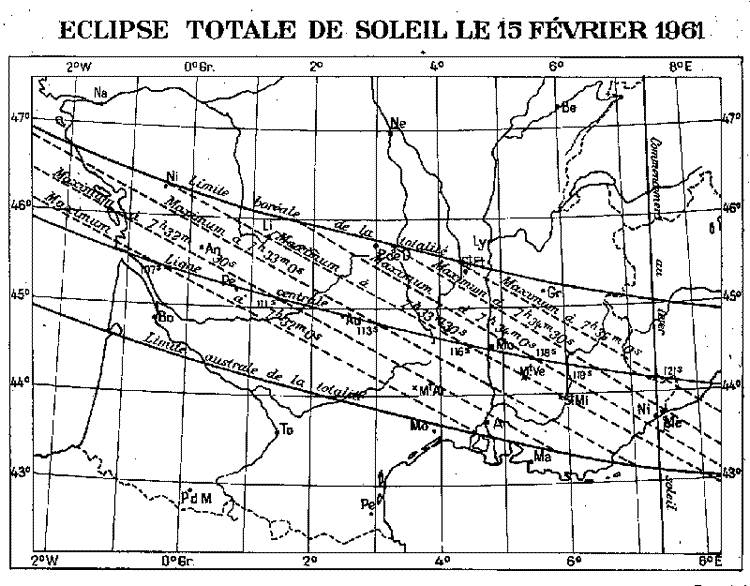
Le 15 février 1961, une éclipse totale a eu lieu dans le midi de la France, au lever du Soleil. On trouvera ci-après les cartes des zones de visibilité ainsi que les horaires.

Le 11 août 1999, une éclipse totale fut visible un peu au nord de Paris entre 10h 20m et 10h 30m Temps Universel. Malheureusement les nuages gênèrent l'observation de ce phénomène.

Pour obtenir les cartes de la zone de visibilité cliquez ici.
 

Liens pour en savoir plus

 

Des explications sur le phénomène"éclipse de Soleil" et "éclipse de Lune"

Les éclipses de Soleil à venir et les éclipses de Lune

Le canon de toutes les éclipses de Soleil de -1999 à l'an 3000 sur le site de la NASA http://eclipse.gsfc.nasa.gov/SEcat5/SEcatalog.html

Le canon de toutes les éclipses de Lune de -1999 à l'an 3000 sur le site de la NASA http://eclipse.gsfc.nasa.gov/LEcat5/LEcatalog.html

 

Bibliographie sommaire : principaux textes de référence

 

Aristote, Traité du ciel, texte grec et trad. fr. par P. Moraux, Paris, Les Belles Lettres, 1965.
Géminos, Introduction aux phénomènes, texte grec et trad. fr. par G. Aujac, Paris, Les Belles Lettres, 1975.
Pline l'Ancien, Histoire naturelle, livre II, texte latin et trad. fr., par J. Beaujeu, Paris, Les Belles Lettres, 1950.
Ptolémée : la seule traduction fiable est celle donnée en langue anglaise par G. J. Toomer sous le titre The Almagest, Londres, Duckworth, 1984.
Jean de Sacrobosco, De sphaera, texte latin et trad. angl. par L. Thorndike, The Sphere of Sacrobosco and its Commentators, Chicago, 1949.
(N. B. Les textes publiés aux éditions Les Belles Lettres sont tous disponibles. On trouvera des extraits en français de certains ouvrages cités ici dans l'anthologie publiée par J.-P. Verdet sous le titre Astronomie & Astrophysique [Textes essentiels], Paris, Larousse 1993).

 

---

Crédit : M. Lerner/D. Savoie/J.E. Arlot/Bureau des longitudes/Observatoire de Paris