










 Français
Français
Comprendre > Concepts fondamentaux
Éclipses de Soleil
Chapitre 2. Les différentes phases d'une éclipse de Soleil
- Circonstances générales d'une éclipse
- Circonstances locales d'une éclipse
- Paramètres et théories utilisés dans les calculs de prédiction des éclipses de Soleil
- Liste des tableaux et des cartes
- Corrections liées à l'échelle de temps utilisée
- Cartes générales et locales
1. Circonstances générales d'une éclipse
Les circonstances générales d'une éclipse correspondent à différentes phases de l'éclipse, qui sont les suivantes :
- le commencement et la fin de l'éclipse générale, ce sont les deux instants et les deux lieux sur Terre où le cône de pénombre de la Lune est tangent extérieur à la surface terrestre,
- le commencement et la fin de l'éclipse totale ou annulaire, ce sont les deux instants et les deux lieux sur Terre où le cône d'ombre de la Lune est tangent extérieur à la surface terrestre,
- le commencement et la fin de la centralité, ce sont les deux instants et les deux lieux sur Terre où l'axe du cône d'ombre de la Lune est tangent à la surface terrestre,
- le maximum de l'éclipse, c'est l'instant et le lieu sur Terre où la grandeur de l'éclipse est maximum,
- et l'éclipse centrale à midi ou minuit vrai, c'est l'instant et le lieu sur Terre où le maximum de l'éclipse se produit lorsque le Soleil dans le plan du méridien,.
2. Circonstances locales d'une éclipse
Il ne faut pas les confondre avec les circonstances générales décrites dans le paragraphe précédent. Les circonstances locales d'une éclipse décrivent, en un lieu donné, les différentes phases de l'éclipse, observables par un observateur situé en ce lieu (Figs. 10 et 11).
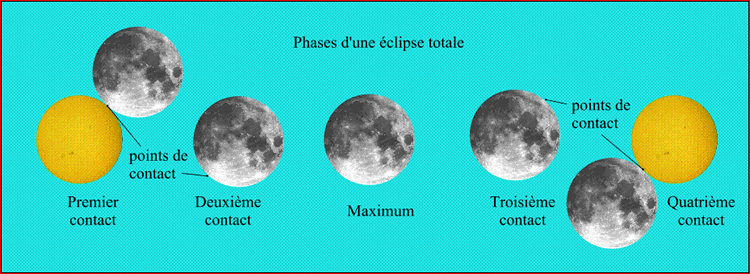
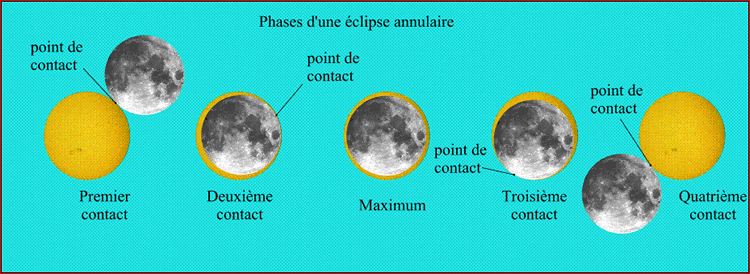
Ces phases sont les suivantes :
- le début de l'éclipse partielle, appelé également premier contact (parfois premier contact extérieur),
- le début de l'éclipse totale ou annulaire (si l'observateur est dans la bande de centralité), appelé également deuxième contact (parfois premier contact intérieur),
- le maximum de l'éclipse, instant où la grandeur est maximum en ce lieu,
- la fin de l'éclipse totale ou annulaire (si l'observateur est dans la ligne de centralité), appelée également troisième contact (parfois deuxième contact intérieur),
- la fin de l'éclipse partielle, appelée également quatrième contact (parfois deuxième contact extérieur).
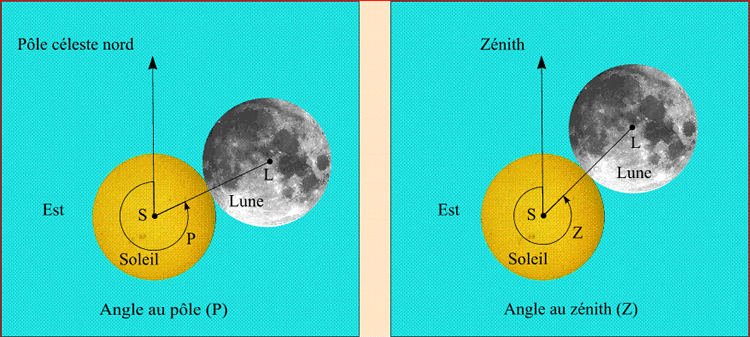
L'angle au pôle P d'un contact est l'angle de la direction nord N (partie boréale du cercle horaire du centre S du Soleil) avec l'arc de grand cercle joignant les centres S et L du Soleil et de la Lune, compté positivement vers l'est, dans le sens nord-est-sud-ouest (Fig. 12).
L'angle au zénith Z d'un contact
a une définition analogue à celle de P, en remplaçant
le cercle horaire du centre S du Soleil par le vertical du même
point (Fig. 12).
Remarque : sous nos latitudes (en France), le Soleil
se trouve souvent au sud, donc quand on regardele Soleil, l'ouest est à
droite du Soleil et l'est est à sa gauche. La Lune éclipse
le Soleil d'ouest en est (donc de la droite vers la gauche lorsque l'on
regarde le Soleil). Pour des latitudes négatives (dans l'hémisphère
sud), l'aspect du phénomène est inversé, l'éclipse
a, bien évidemment, toujours lieu d'ouest en est, mais elle a lieu
de la gauche vers la droite car le Soleil est au nord.
Pour le maximum on donne également la grandeur de l'éclipse, le degré d'obscurité, la hauteur h et l'azimut a du Soleil.

À un instant donné la grandeur g de l'éclipse est l'inverse du rapport du diamètre du Soleil sur la distance du bord du Soleil le plus rapproché du centre de la Lune au bord de la Lune le plus rapproché du centre du Soleil (Fig. 13).
Le degré d'obscurité est le pourcentage de la surface du disque solaire éclipsé par la Lune (Fig.13).
La hauteur h du Soleil sur l'horizon est l'angle de la direction du Soleil et du plan horizontal, compté en degrés de -90° à +90°. Dans nos tableaux, on ne tient pas compte de la réfraction atmosphérique.
L'azimut est l'angle formé par la projection de la direction du Soleil dans le plan horizontal avec la direction du Sud, compté en degré dans le sens rétrograde (sud = 0°, ouest = 90°, nord = 180°, est = 270°).
Les circonstances locales d'une éclipse peuvent être calculées à l'aide des éléments de Bessel
3. Paramètres et théories utilisés dans les calculs de prédiction des éclipses de Soleil
Les théories utilisées dans les calculs sont les suivantes :
- pour la Lune, la théorie ELP2000 élaborée par M. Chapront-Touzé et J. Chapront (1982),
- pour le Soleil, la théorie VSOP82 élaborée par P. Bretagnon (1982).
On n'utilise pas directement ces théories, mais des éphémérides de ces corps, qui se présentent sous la forme de séries de développements en polynômes de Tchebychev (G. Francou et al. 1987).
L'échelle de temps utilisée dans les calculs
d'éphéméride est le Temps terrestre (TT).
Les prédictions sont données dans un repère
lié à la Terre, les positions des lieux sur Terre sont données
en latitudes et en longitudes géographiques, les longitudes sont
exprimées par rapport au méridien de Greenwich, positivement
vers l'ouest et négativement vers l'est. Les instants des différentes
phases de l'éclipse sont donnés en Temps universel (UT).
Pour cela, il est nécessaire d'avoir pour chaque éclipse
une approximation de la différence entre ces deux échelles
de temps.
Dans le calcul des circonstances intervient également
un certain nombre de paramètres physiques.
Ces paramètres sont les suivants :
- la parallaxe horizontale du Soleil à une unité astronomique,
- le demi-diamètre solaire,
- le rapport du rayon lunaire sur le rayon équatorial terrestre,
- le rayon équatorial terrestre,
- le carré de l'ellipticité terrestre.
4. Liste des tableaux et des cartes
Tous les instants publiés sont en Temps universel (pour les éclipses futures, valeurs extrapolées de UT1), toutes les longitudes sont comptées à partir du méridien de Greenwich, positivement vers l'ouest et négativement vers l'est.
Pour chaque éclipse de Soleil on donne les renseignements suivants :
- Les éphémérides de la Lune et du Soleil le jour et le lendemain de l'éclipse, ce sont les coordonnées équatoriales géocentriques apparentes. On donne également l'écart en ascension droite entre la Lune et le Soleil.
- Les différents paramètres utilisés dans le calcul, notamment la valeur Dte qui est la différence estimée entre le Temps terrestre et le Temps universel le jour de l'éclipse.
- Les circonstances générales de l'éclipse.
- Les éléments de Bessel sous forme polynomiale et sous forme tabulée (notations française et américaine).
- Les limites de la bande de centralité (limites nord et sud de l'ombre), la ligne de centralité, la durée de l'éclipse sur la ligne de centralité, ainsi que la hauteur (h) du Soleil au moment du maximum.
- Les circonstances locales sur la ligne centrale. Pour un instant donné on fournit :
- Des tableaux de circonstances locales pour différents pays.
- - la durée de la phase centrale (totale ou annulaire),
- L la largeur de l'ombre sur la Terre dans la direction perpendiculaire à son déplacement,
- le degréd'obscurité (Obs.),
- la grandeur de l'éclipse (g),
- la hauteur (h) et l'azimut (a) du Soleil,
- les coordonnées géographiques du point correspondant.
- et pour chaque contact on donne :
- - l'instant du contact,
- l'angle au pôle P
- l'angle au zénith Z.
Pour chaque ville on donne :
- - les coordonnées géographiques de la ville
(en degré et minute de degré),
- le nom de la ville,
- la durée de la phase centrale (si elle existe),
- l'instant du maximum avec le degré d'obscurité (Obs.),
- la grandeur de l'éclipse (Mag.),
- la hauteur (h) et l'azimut (a) du Soleil,
- et pour chaque contact on donne
- - l'instant du contact;
- l'angle au pôle P
- l'angle au zénith Z.
5. Corrections liées à l'échelle de temps utilisée
Il faudra effectuer les corrections apportéespar une meilleure connaissance de l'écart Temps terrestre (TT) - Temps universel (UT1).
En effet, tous les calculs sont faits à partir
d'une estimation de cet écart Dte
. Les prévisions étant faites de nombreuses années
à l'avance, il arrive que la valeur réelle de cet écart
Dtr
diffère de sa valeur estimée.
Dans ce cas on doit corriger les résultats publiés
de la manière suivante :
Soit dt = Dtr - Dte la différence entre la valeur réelle et la valeur estimée.
Les instants des phénomènes doivent être corrigés de dt, et les longitudes géographiques des phénomènes doivent être corrigées de d l = -1,002738 x dt (l et d t étant dans la même unité). Attention, on corrige les longitudes des lieux liés aux différentes phases et courbes et non les longitudes des lieux des villes dans les tableaux de circonstances locales.
6. Cartes générales et locales
Pour chaque éclipse, on donne une ou plusieurs cartes générales de l'éclipse. Sur ces cartes on fait figurer les courbes suivantes : la bande de centralité (lorsqu'elle existe), les limites boréale et australe de l'éclipse, les courbes de commencement, de fin et de maximum aux lever et coucher du Soleil, ainsi que les courbes de commencement et fin pour un instant donné (toutes les heures en général). Pour le tracé de cette carte, on utilise une projection stéréographique, c'est-à-dire une projection azimutale conforme. Cette projection permet d'avoir une représentation des pôles sur la carte.
On donne également, un certain nombre de cartes
locales. Sur ces cartes, lorsqu'elles sont présentes, on donne,
en plus, les courbes de commencement, de fin et de maximum à un
instant donné (avec un pas plus adapté à la carte),
et parfois la projection de l'ombre à des instants donnés.
Les cartes locales sont tracées à l'aide de différentes
projections en fonction du lieu représenté (projection conforme
de Lambert, projection de Mercator...).
Ci-dessous, dans le cas de l'éclipse du 11 août 1999,
l'ombre portée par la Lune sur la Terre se déplace, traçant
la bande de centralité. La pénombre trace les contours des
zones d'où l'on aperçoit l'éclipse partielle.
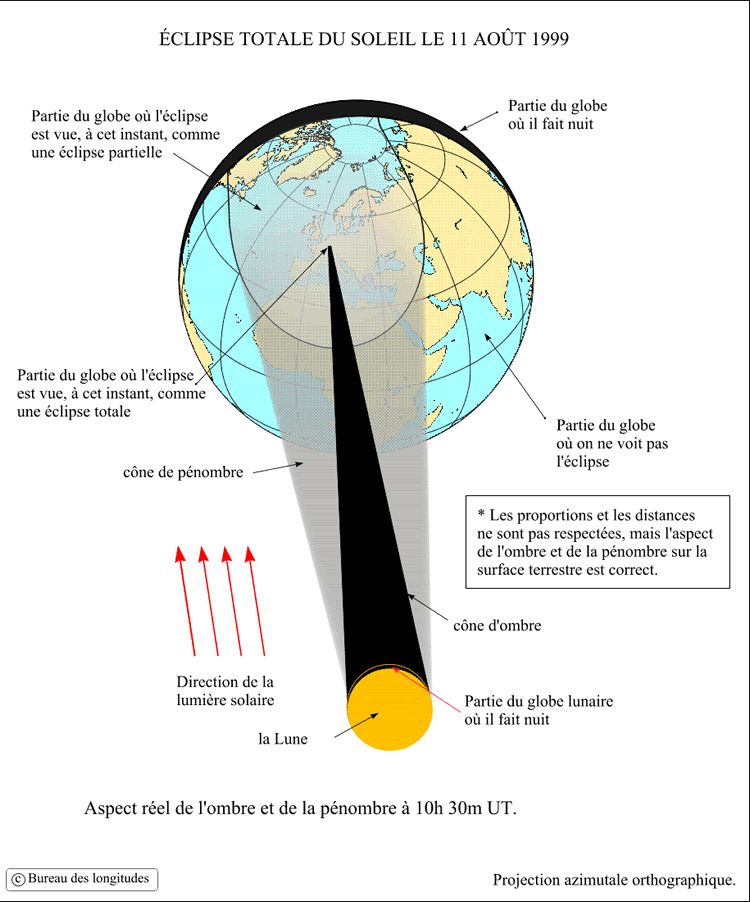
Crédit : P. Rocher/IMCCE