L'OBSERVATION INFRAROUGE

Ce qui suit ne concernera que le domaine infrarouge. En effet, le domaine visible a été abondamment étudié puisqu'il a été longtemps le seul auquel nous ayons eu accès - on ignorait même, autrefois l'existence des autres -. Le domaine radio fait appel aux techniques des oscillateurs à très courte longueur d'onde très différents : on n'est plus dans le domaine optique. Il en est de même des domaines des rayons X et gamma.

La loi de Planck

La grande loi physique qui est prépondérante dans ce domaine est la suivante : Tout corps chauffé émet un rayonnement électromagnétique bien défini, dans un ensemble de longueurs d'onde qui ne dépend que de la température. Dite sous cette forme, elle autorise tout physicien digne de ce nom à hurler, mais, pour notre propos, elle nous conviendra parfaitement. Par contre il est impératif de définir ce que nous entendons par température. Il ne s'agit pas des températures de la vie quotidienne, dont le zéro est défini comme la température de la glace fondante et le "cent" comme la température de l'eau à l'ébullition. Il s'agit de températures absolues mesurant le degré d'agitation des molécules composant le corps considéré. Dans cette échelle de température, le zéro des températures ordinaires correspond à 273 degrés absolus que l'on note 273 K et que l'on prononce K ou Kelvin.

Si λ est la longueur d'onde reçue d'un corps émissif à la température T, correspondant au rayonnement maximum, alors :

λ x T = constante

Si λ est en micromètres et T en kelvins, alors la constante est égale à 3000

Pour chaque valeur de la température, l'intensité du rayonnement en fonction de la longueur d'onde est représentable par une courbe qui a grossièrement la forme d'un chapeau de gendarme. Elle part de la valeur zéro pour une valeur de la longueur d'onde, croît jusqu'à une valeur maximum puis décroît, plus rapidement qu'elle a cru, pour retourner à la valeur zéro à une autre valeur de la longueur d'onde supérieure à la précédente. La valeur du maximum augmente si la température augmente et la position de ce maximum se déplace alors vers les longueurs d'onde plus courtes.

Dans le domaine visible, donc pour notre oeil, l'impression sur la rétine sera grossièrement celle de la couleur correspondant au maximum de la courbe. Si nous observons attentivement le ciel à l'oeil nu nous constatons que certaines étoiles apparaissent rouges alors que d'autres semblent être franchement bleues. De ce que nous avons dit précédemment, nous pouvons conclure que les étoiles bleues sont plus chaudes que les rouges (puisque le bleu a une plus courte longueur d'onde que le rouge).

Cette courbe et la loi qu'elle représente, ainsi que la fonction qui exprime cette loi sont connues sous le nom de "loi de rayonnement du corps noir". Sous sa forme définitive, elle a été découverte par le physicien allemand Max Planck (1858-1947) pour laquelle il obtint, en 1918, le Prix Nobel de physique. Cette loi contient une constante, désignée par la lettre "h", appelée constante de Planck, qui est une des cinq ou six constantes les plus importantes de toute la physique.

Les contraintes que nous impose la loi de Planck.

Revenons à nos observations. Nous disposons d'un télescope et d'un récepteur qui peut être, par exemple, une caméra destinée à faire de l'imagerie. Notre programme est l'observation dans l'infrarouge. Notre télescope est sur terre en un lieu où la température extérieure est, disons, voisine de zéro. Sa température absolue est donc de 273K. Et c'est ici que les difficultés commencent. Car, à cette température, le télescope rayonne (il brille) de l'énergie dans un domaine de longueurs d'onde qui est précisément celui dans lequel nous voulons travailler. Le télescope et également tout ce qu'il y a autour de lui, la coupole et le ciel (l'atmosphère). Et également le récepteur.

Que faire ? Prenons les problèmes un par un. Le récepteur est placé dans un cryostat; c'est une enceinte très particulière qui permet de maintenir à très basse température les équipements qu'elle contient. En astronomie, on utilise des cryostats refroidis à l'hélium liquide. On obtient ainsi les plus basses températures que l'on sache faire de façon relativement simple, quelques degrés Kelvin seulement. A ces températures, le rayonnement propre du récepteur n'introduit plus aucune gêne, mais l'utilisation d'un tel cryostat entraîne une importante complication.

Le télescope ? S'il est possible de placer un récepteur de quelques millimètres de côté dans un cryostat, il n'en va pas de même d'un télescope pesant plusieurs dizaines de tonnes. On lève la difficulté en construisant des télescopes dont la configuration optique est telle, que la seule chose que "voit" le récepteur est le ciel. Tout rayonnement dû au télescope est ainsi éliminé. Remarquons tout de même que, là, le résultat n'est pas aussi parfait que pour le cas du récepteur. Il reste dans le champ des éléments impossibles à masquer comme l'araignée qui maintient en place le miroir secondaire du télescope. Faute de pouvoir faire autrement, et parce que l'énergie rayonnée par ces éléments est faible on se contente de cette solution. C'est un bon exemple des compromis que l'observateur est obligé de faire pour avancer. Il ne faudra pas oublier, au moment de l'analyse des résultats, que ce compromis introduit une erreur à prendre en compte.

Le ciel aussi rayonne de l'énergie que voit le récepteur. Celle-ci s'ajoute à l'énergie de l'objet observé. On pourrait donc penser la mesurer une fois pour toute en observant le ciel à côté de l'objet en dépointant légèrement le télescope pour que cet objet sorte du champ. Ceci ne nous servirait à rien car le rayonnement propre du ciel fluctue rapidement et sa mesure est à faire en permanence. On a résolu ce problème en faisant vibrer le miroir secondaire de façon qu'il passe de la configuration "objet dans le champ" à la configuration "objet hors du champ" quelques dizaines de fois par seconde. On a ainsi, dans une des positions, le flux du ciel seul et dans l'autre, la somme des flux de l'objet à observer et du ciel. Une électronique spécialement prévue à cet effet retranche automatiquement le flux dû au ciel. On fait alors ce que l'on appelle de la "détection synchrone".

Signalons que depuis le sol, toutes les longueurs d'onde infrarouges ne sont pas observables. L'atmosphère terrestre est opaque pour certaines d'entre elles et nous ne disposons que de "fenêtres" d'observation caractérisées par leur longueur d'onde et désignées par une lettre.

Fenêtres d'observation IR : transmission de l'atmosphère terrestre mesurée à l'observatoire de Kitt Peak

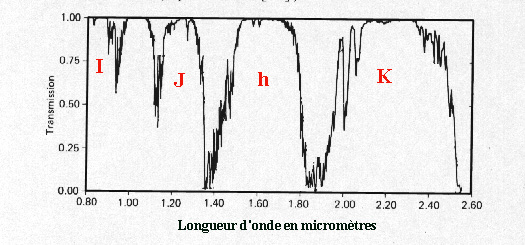
Premier exemple de ce que peut nous apprendre l'observation dans l'infrarouge : la planète Jupiter

Les planètes du système solaire sont des corps d'autant plus froids qu'ils sont plus loin du Soleil, ce dernier étant la source de toutes les formes d'énergie qui se manifestent dans le système solaire. Si les planètes brillent, c'est parce que leurs sols ou leurs atmosphères réfléchissent, à la manière d'un miroir, l'énergie qu'elles reçoivent du Soleil. Le Soleil ayant son maximum d'énergie dans le jaune - à 0.5 microns, il en va de même des planètes. En plus de ce rayonnement réfléchi, une planète doit montrer un rayonnement "de corps noir" conforme à la loi de Planck et dû à sa température. Or, on a eu l'idée d'observer Jupiter, la planète la plus massive - et aussi la plus grosse, - dans l'infrarouge. A la distance à laquelle elle se trouve du Soleil, sa température n'est que de 130°K. A cette température correspondent les longueurs d'onde du domaine radio. En infrarouge, Jupiter devait donc être complètement "noire". Or elle apparut "brillante". La seule explication possible est que Jupiter possède, en son centre, une quantité de matière qui, sous l'effet des fortes pressions dûes aux poids des couches extérieures, est portée à une température élevée et qui rayonne de l'énergie dans l'infrarouge. Connaissant la longueur d'onde de ce rayonnement et la masse de la planète, on a pu, par le calcul, se faire une idée de ce que devait être le coeur de cette planète. On s'est alors rendu compte que Jupiter a raté de peu d'être une étoile. Si la masse de Jupiter avait été plus importante, les pressions au centre de la planète auraient, alors, été suffisantes pour élever la température jusqu'au million de degrés nécessaire pour amorcer les réactions thermonucléaires et transformer la planète en étoile, c'est-à-dire un corps capable de rayonner de l'énergie par lui-même. Dans son état actuel, Jupiter n'est qu'une "proto-étoile".

Deuxième exemple d'observation infrarouge : Io, satellite galiléen de Jupiter

Les sondes spatiales ont mis en évidence un volcanisme très actif à la surface du premier satellite de Jupiter, Io. Malheureusement, l'observation directe depuis la Terre est impossible : ces volcans sont trop petits (diamètre de quelques kilomètres, inférieur au pouvoir de résolution des télescopes). Cependant tout ceci est vrai dans le rayonnement visible en provenance du Soleil que le satellite Io réfléchit. Mais la chaleur de ces sources volcaniques en fait des émetteurs. Cette émission est-elle observable depuis la Terre ? La réponse est oui grâce aux observations dans l'infrarouge. Pour comprendre comment nous allons effectuer les observations il faut se rappeler la loi

λ x T = 3000 micromètres x Kelvin

où λ est la longueur d'onde émise par le corps et T la température de ce corps, correspondant au maximum de rayonnement.

Dans le cas du rayonnement solaire réfléchi par Io, le maximum est à 0,5 micromètre et baisse en allant vers l'infrarouge et est pratiquement nul vers 3 micromètres. D'autre part, le satellite lui-même n'est pas complètement froid : sa température de surface varie de 90K (la nuit) à 125K (le jour) et son rayonnement thermique est émis à 15 micromètres. Par contre, les volcans apparaissent comme autant de points chauds à 300K rayonnant à 10 micromètres comme le montre la figure ci-dessous et même à partir de 3.6 micromètres qui correspond à une fenêtre de visibilité de l'infrarouge depuis le sol.

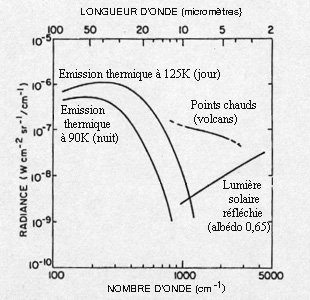
Des observations d'occultation de Io par un autre satellite galiléen ont confirmé cette possibilité et montré l'activité et la position des volcans depuis la Terre.