Réduire la taille du texte du contenu Aggrandir la taille du texte du contenu Imprimer cette page English

Comprendre > Concepts fondamentaux

Éclipses de Soleil

Chapitre 3. Calcul des circonstances locales d'une éclipse de Soleil




  1. Définition des éléments de Bessel
  2. Calcul des circonstances locales
    1. Calcul de la grandeur maximale en lieu
    2. Calcul des instants des contacts en un lieu : 
    3. Calcul de l'angle au pôle et de l'angle au zénith


1. Définition des éléments de Bessel


Pour un lieu donné il y a lieu de déterminer : 

  • les instants des différents contacts,
  • l'instant du maximum de l'éclipse et la grandeur de l'éclipse à cet instant,
  • les angles au pôle et au zénith de chacun des contacts.
 

  Fig 14 : Définition des éléments de Bessel 
Le lieu d'observation est défini par sa longitude l (positive à l'ouest et négative à l'est du méridien de Greenwich), sa latitude j et son altitude h au-dessus du niveau de la mer.

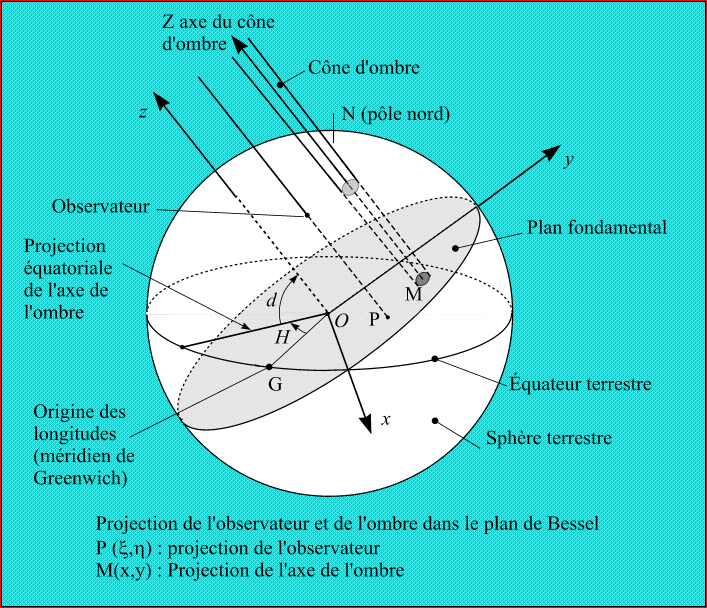
On définit à chaque instant un système de coordonnées Oxyz de sens direct, dans lequel : 

O est le centre de la Terre.

L'axe Oz est parallèle à l'axe des cônes de pénombre et d'ombre, le sens positif étant celui qui va de la Terre à la Lune.

L'axe Ox est l'intersection du plan fondamental Oxy perpendiculaire à Oz et du plan de l'équateur terrestre, le sens positif étant vers l'est.

L'axe Oy est normal à Ox dans le plan fondamental, le sens positif étant vers le Nord.

En utilisant comme unité de longueur le rayon équatorial terrestre, les éléments de Bessel sont définis de la manière suivante : 

x, y, z sont les coordonnées du centre de la Lune.

d et H sont la déclinaison de l'axe Oz et son angle horaire par rapport au méridien de Greenwich.

fe et fi sont les demi-angles au sommet des cônes de pénombre et d'ombre, fe étant pris par convention positif et fi négatif.

ue et ui sont les rayons des sections circulaires des cônes de pénombre et d'ombre par le plan fondamental Oxy et s'obtiennent par les formules suivantes : 

    ue = z . tan fe + k . séc fe
    ui = z . tan fi + k . séc fi
où k est le rayon de la Lune exprimé en rayon équatorial terrestre.

Les coordonnées x, h, z du lieu d'observation dans le système Oxyz sont : 

     x = r . cos j' . sin (H - l ),
    h = r . sin j' . cos d - r . cos j' . sin d . cos ( H - l ),
    z = r . sin j' . sin d + r . cos j' . cos d . cos ( H - l ),
avec : 

 

    r . cos j' = cos u + h/r0 . cos j
    r . sin j' = (1 - f) . sin u + h/r0 . sin j
et
    tan u = (1 - f) . tan j,
où h est l'altitude du lieu exprimée en mètres, r0 est le rayon équatorial terrestre exprimé en mètres et f l'aplatissement de l'ellipsoïde terrestre (f = 1/298,257 = 0,003 35281).

Les variations horaires x', h', z' de ces coordonnées sont fournies avec une précision de l'ordre de la seconde de temps par les formules suivantes, H' étant exprimé en radians par heure.

    x' = H' . r . cos j' . cos (H - l ),
    h' = H' . x . sin d,
    z' = - H' . x . cos d,
Les rayons le et li des sections circulaires des cônes de pénombre et d'ombre par le plan mené par le lieu d'observation parallèlement au plan fondamental s'obtiennent par les formules suivantes : 
    le = ue - z tan fe
    li = ui - z tan fi



2. Calcul des circonstances locales


Chaque élément de Bessel que l'on pourra désigner par b est représenté sur un intervalle de temps (t0, t1) par des coefficients de développements en polynômes du temps, à l'exception de tan fe et de tan fi qui sont considérées comme constantes sur l'intervalle. Un élément de Bessel se calcule à un instant t par la formule : 

    b = b0 + b1 . T + b2 . T2 + b3 . T3
avec T = t - t0.

 T, exprimé en heure, représente le temps écoulé depuis l'instant origine t0.

La variation horaire b' d'un élément de Bessel se calcule par la formule : 

 

    b' = b1 + 2 b2 . T + 3 b3 . T2



2.1. Calcul de la grandeur maximale en un lieu


Soient : 

    U = x - x, U' = x' - x',
    V = y - h, V' = y' - h',
On prend comme valeur de départ td l'époque du maximum de l'éclipse, l'instant du maximum tm se calcule en ajoutant à td la valeur Dtm donnée par : 
    Dtm = - (UU' + VV') / (U'2 + V'2)
On doit réitérer le calcul en prenant comme nouvelle valeur de départ la valeur de tm.

La grandeur maximale est donnée par : 

    g = (le - lm) / (le - li)
pour une éclipse annulaire ou totale au lieu considéré, ou : 

 
    g = (le - lm) / (2 le - 0,5465)
pour une éclipse partielle, avec : 

 

    lm = (U2 + V2)½


2.2. Calcul des instants des contacts en un lieu


On prend comme valeurs de départ td du premier et du quatrième contacts (contacts extérieurs) des valeurs approchées déduites de la carte de l'éclipse et l'on prend comme valeurs de départ du second et du troisième contacts (contacts intérieurs), lorsqu'ils existent, la valeur tm du maximum calculée précédemment.

Pour chaque valeur td de départ on calcule les quantités suivantes :  

    b = (UU' + VV') / (U'2 + V'2),
    g = (U2 + V2 - l2) / (U'2 + V'2),
    q = ± (b2 - g)½
avec l = le ou l = li et q étant du signe de b.

Les instants du premier et du quatrième contacts se calculent par la formule : 

 

    t = td - b + q
et les instants du second et du troisième contacts se calculent par les formules : 

 

    t = td - b - | q | pour le second contact,
et
    t = td -  b + | q | pour le troisième contact.
Comme pour le calcul du maximum on doit réitérer les calculs en prenant comme nouvelles valeurs de départ les valeurs t.



2.3. Calcul de l'angle au pôle et de l'angle au zénith


La valeur de l'angle au pôle P d'un point de contact est donnée par : 
 

    tan P = U/V ,
où sin P a le signe de U, sauf pour les second et troisième contacts (contacts intérieurs) d'une éclipse totale pour lesquels sin P est de signe contraire à U.

L'angle au zénith Z d'un point de contact est donné par : 
 

    Z = P - G ,
en désignant par G l'angle parallactique défini d'une façon approchée par : 

 

    tan G = x / h,
sin G étant du signe de x.


Crédit : P. Rocher/IMCCE